Mol

O mol ^{(português brasileiro)} ou a mole ^{(português europeu)} é o nome da unidade de base do Sistema Internacional de Unidades (SI) para a grandeza quantidade de matéria ^{(português brasileiro)} ou quantidade de substância ^{(português europeu)} (símbolo: mol). É uma das sete unidades de base do SI muito utilizada na Química.

Seu uso é comum para simplificar representações de proporções químicas e no cálculo de concentração de substâncias.

A unidade mol é muitas vezes comparada à "dúzia", pois ambas são adimensionais (sem unidades) e são utilizadas para descrever quantidades. Porém, o uso do mol mostra-se adequado somente para descrever quantidades de entidades elementares (átomos, moléculas, íons, elétrons, outras partículas, ou grupos específicos de tais partículas).

Índice

1 História

1.1 Evoluções da definição

2 Entidades elementares

3 Grafia e plural

4 Mol e a constante de Avogadro

5 Mol e massa molar

6 Mol e volume molar

7 Utilidade do mol

7.1 Comparações com a "dúzia"

8 Diferenças entre mol e molécula

9 O tamanho do mol

9.1 Entidades do dia-a-dia

10 Referências

11 Bibliografia

História

Professor A.W. Hofmann

O termo molar (do latim moles, que significa "grande massa") foi inicialmente introduzido na química pelo químico alemão August Wilhelm Hofmann, por volta de 1865. O termo foi introduzido para indicar uma grande massa macroscópica, contrariando assim a palavra "molecular" (palavra também derivada de moles, pela adição do sufixo "-cula", significando "pequeno" ou "diminuto"). Esse uso particular do termo molar foi se tornando comum na literatura física por volta do ano de 1940.

O uso mais restrito do termo molar, significando não somente uma amostra macroscópica, mas preferivelmente uma massa em gramas que reflete a massa de todas as moléculas contidas, bem como o uso da terminologia "mol", é geralmente atribuído ao físico-químico alemão Wilhelm Ostwald. Este termo aparece em vários livros científicos do século XX. De forma irônica, o uso do termo empregado por Ostwald esteve relacionado com sua crítica à teoria atômico-molecular e sua tentativa de estabelecer uma alternativa macroscópica para a discussão das leis estequiométricas. Embora o uso da definição de volume molar dos gases (22,4 L nas CNTP) tenha aparecido mais cedo — início do século XX em livros norte-americanos — a interconversão explícita de mol para grama, com o objetivo de facilitar na resolução de problemas estequiométricos, foi mais comum após 1950.

Como uma nota linguística, é interessante saber que o termo "mol" também foi utilizado pelos romanos para se referir às pesadas pedras usadas para construir barragens marítimas e de moinhos. A posterior conexão linguística com o ato de moer também ocorre em outros casos, como em "dentes molares".

Evoluções da definição

Wilhelm Ostwald

Antes de 1959, tanto a União Internacional de Física Pura e Aplicada (IUPAP) quanto a União Internacional de Química Pura e Aplicada (IUPAC) usavam o oxigênio para definir a grandeza quantidade de matéria, sendo definida como o número de átomos existentes em 16 g de oxigênio que possui massa de 16 g. Os físicos usaram uma definição similar a esta, porém, fazendo uso do isótopo do oxigênio de massa 16 (oxigênio-16). Posteriormente as duas organizações entraram em um acordo, entre 1959 e 1960, e definiram a unidade de medida da grandeza quantidade de matéria como:

"Mol é a quantidade de matéria de um sistema que contém tantas entidades elementares quanto são os átomos contidos em 0,012 quilograma de carbono-12; seu símbolo é "mol".^[1]

Como adendo a esta definição, a IUPAC esclarece que, quando a terminologia mol for usada, as entidades elementares devem ser especificadas, podendo ser átomos, moléculas, íons, elétrons, outras partículas, ou grupos especificados de tais partículas.

Essa definição foi adotada pelo CIPM (Comitê Internacional de Pesos e Medidas) em 1967 e, em 1971, ratificada pela XIV Conferência Geral de Pesos e Medidas (Resolução 3, 1971). Em 1980, o CIPM confirmou novamente esta definição, adicionando a informação de que os átomos de carbono-12 não estariam ligados por meio de ligações químicas, mas em seu estado fundamental.

Entidades elementares

Colher de chá contendo 5 mL de água (aproximadamente 0,3 mol de água).

Ao utilizar o termo mol, deve-se especificar quais são as entidades elementares em questão (átomos, moléculas, íons, elétrons, outras partículas ou agrupamentos especificados de tais partículas), uma vez que ambiguidades podem ser geradas.

Por exemplo, se fosse escrito apenas 4,44 mol de hidrogênio, seria impossível saber se significa 4,44 mol de átomos ou de moléculas de hidrogênio. Uma maneira usual e conveniente para contornar possíveis ambiguidades é escrever a fórmula molecular da entidade elementar que está contida pelo mol: 4,44 mol de H₂; 6,28 × 10^–2 mol de PbO; 3 mols de Fe.

Quando a substância é um gás, geralmente as entidades elementares em questão são moléculas. Porém, gases nobres (hélio, neônio, argônio, criptônio, xenônio, e radônio) são monoatômicos nas condições ambientes (ou seja, cada entidade elementar de um gás nobre é um único átomo).

Grafia e plural

O nome para a unidade "mol" deve ser grafado sempre em letra minúscula, assim como em todos os nomes das unidade do SI (exceto "grau Celsius"). Para o emprego do plural, deve-se saber que somente o nome da unidade de medida aceita o plural, que é sempre feito pela adição da letra "s" após o nome da unidade. No Brasil, o nome e o símbolo da unidade de medida da grandeza quantidade de matéria são idênticos, isto é: mol e mol, respectivamente. Isto faz com que o plural do mol (substantivo masculino) seja mols. Em Portugal, o nome da unidade é a mole (substantivo feminino), logo, seu plural é moles.
Exemplo:

	Brasil: Dois mols de uma substância;
	Portugal: Duas moles de uma substância.

O mol como símbolo de unidade não aceita plural^[2].
Exemplos: 10,5 m (e não 10,5 ms), 7,2 L (e não 7,2 Ls); 5,0 mol (e não 5,0 mols).

Como nome da unidade, o plural deve ser empregado da seguinte forma:

	Brasil: Uma solução contém dois mols de íons cloreto (semelhante a: A mesa tem três metros de comprimento);
	Portugal: Uma solução contém duas moles de íons cloreto.

Mol e a constante de Avogadro

Quanto mais assopramos para encher o balão, maior a quantidade de gás (mols) e, conseqüentemente, maior o seu volume. Essa é uma relação direta de proporcionalidade, observada por Avogadro.

O conceito de mol está intimamente ligado à constante de Avogadro (antigamente chamada de número de Avogadro), onde 1 mol tem aproximadamente 6,022 × 10²³ entidades. Este é um número extremamente grande, pois se trata de uma medida da ordem de sextilhões. Exemplos:

	1 mol de moléculas de um gás possui aproximadamente 6,022 × 10²³ moléculas deste gás, ou seja, seiscentos e dois sextilhões de moléculas.
	1 mol de íons equivale a aproximadamente 6,022 × 10²³ íons, ou seja, seiscentos e dois sextilhões de íons.
	1 mol de grãos de areia equivale a aproximadamente 6,022 × 10²³ grãos de areia, ou seja, seiscentos e dois sextilhões de grãos de areia.

Mol e massa molar

A massa molar é a massa em grama de 1 mol de entidades elementares. A massa atômica e a massa molar de uma mesma substância são numericamente iguais. Por exemplo:

	Massa atômica do sódio = 22,99 u (massa de 1 átomo)
	Massa molar do sódio = 22,99 g/mol (massa de 1 mol de átomos)

	Massa atômica do cálcio = 40,078 u (massa de 1 átomo)
	Massa molar do cálcio = 40,078 g/mol (massa de 1 mol de átomos)

Deve-se ainda saber que 1 mol de diferentes substâncias, possui sempre o mesmo número de partículas. No entanto, a massa contida em 1 mol varia consideravelmente entre as substâncias.

Mol e volume molar

Esfera de silício

Volume molar é a razão entre o volume e a quantidade de matéria. Equivale ao volume ocupado por 1 mol de entidades elementares, podendo estar no estado gasoso ou sólido. Nas CNTP e nas CPTP o volume molar de um gás ideal é de aproximadamente 22,4 e 22,7 litros, respectivamente^[3]. Para o silício sólido, o volume molar é de aproximadamente 12,06 litros^[4].

Em um dos experimentos realizados por Avogadro, foi observado que o volume de um gás é diretamente proporcional ao número de suas partículas. Isto significa que, quanto maior a quantidade de entidades elementares de um gás, maior será o volume ocupado.

Utilidade do mol

Balança analítica com um béquer de 50 mL em seu interior contendo ca. 1 mol de NaCl (58,44 g).

O mol é utilizado para simplificar representações de proporções químicas. A uma dada massa (por exemplo, 1,0 g) de cada uma das diferentes substâncias sempre estão associados números distintos e extremamente grandes das entidades que compõem essas substâncias. Isto porque essas entidades (sejam moléculas, átomos ou fórmulas unitárias) têm massas distintas. Entretanto, ao químico interessa trabalhar com um número fixo de entidades. Para isso, ele dispõe da grandeza denominada "quantidade de matéria" (uma das sete grandezas de base do SI), cuja unidade é o mol.
Em uma representação de uma reação química, as fórmulas moleculares das substâncias são precedidas por números, chamados de coeficientes, que têm como função, indicar as proporções adequadas das substâncias participantes desta reação. Por exemplo, na combustão do gás hidrogênio, temos:

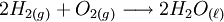
$2H_{2 (g)} + O_{2 (g)} \longrightarrow 2H_2O_{(\ell )}$

Há uma proporção mínima de duas partes de gás hidrogênio para cada uma parte de gás oxigênio, formando duas partes de água. Em se tratando de mols, para cada dois mols de gás hidrogênio que reagem com um mol de gás oxigênio, tem-se como produto dois mols de água líquida.

Numa visão microscópica, aproximadamente 1,2044 × 10²⁴ (1 septilhão, 200 sextilhões) moléculas de gás hidrogênio reagem com 6,022 × 10²³ (seiscentos e dois sextilhões) moléculas de gás oxigênio, formando 1,2044 × 10²⁴ moléculas de água.

Comparações com a "dúzia"

Apesar de não ser recomendada, a comparação com a "dúzia" facilita na compreensão da utilidade do mol. Partindo de exemplos do dia-a-dia, quando se compra 60 laranjas, tem-se:

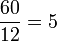$\frac{60}{12} = 5$ dúzias de laranjas

Desta forma, torna-se simples e prático lidar com o conceito de dúzia ao invés de imaginar um número tão grande de laranjas. Se os químicos também utilizassem do conceito da dúzia para simplificar o número de átomos existentes em 56 g de ferro, que contém aproximadamente a quantidade de Avogadro de átomos, ou seja, 6,02 × 10²³ átomos de ferro, teriam como resultado:

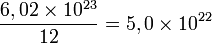$\frac{6,02 \times 10^{23}}{12} = 5,0 \times 10^{22}$ dúzias de átomos

Percebe-se, assim, que, se utilizar da dúzia para medir a quantidade de átomos, a grandeza numérica praticamente não será alterada.

Como átomos, moléculas e outras entidades elementares possuem dimensões muito reduzidas e uma pequena quantidade de matéria assume números extremamente grandes de entidades, torna-se conveniente contar a quantidade de matéria em grupos de 6,02 × 10²³ (constante de Avogadro). Sendo assim, 6,02 × 10²³ átomos de ferro equivalem a 1 mol de átomos de ferro.

Diferenças entre mol e molécula

Comparação entre molécula e mol para a substância gás carbônico (CO₂).

Ambas as palavras mol e molécula têm sua origem no latim moles, que entre seus muitos significados, traz a idéia de "porção", "quantidade", "massa" ou "grande massa".

Porém, não se deve confundir o conceito de mol com o de molécula. Para evitar esta confusão, deve-se lembrar que mol refere-se a uma quantidade de entidades elementares (aproximadamente 6,022 × 10²³ entidades, ou seiscentos e dois sextilhões de entidades) enquanto que molécula (palavra originalmente derivada do diminutivo de mol), refere-se à menor parte da substância que ainda é considerada aquela substância.

Exemplo: Um mol de água (ou da substância água) tem aproximadamente 18 g. Imaginando o mundo "microscópico", isso significa dizer que 18 g de água tem 6,022 × 10²³ (seiscentos e dois sextilhões) moléculas de água.

Outra confusão que pode ocorrer é com relação às grandezas massa molar e massa molecular. A massa molar (representada pela letra "M") indica a massa, em gramas, de 1 mol de qualquer entidade elementar, já a massa molecular, refere-s à massa de uma única molécula de uma substância, representada por unidade de massa atômica "u".

O tamanho do mol

Visão parcial de uma proveta contendo 18 mL de água (1 mol de água).

Apesar de ser um número extremamente grande de entidades elementares, um mol de uma substância pode se referir a um pequeno volume. Para a substância água, por exemplo, 1 mol de água líquida ocupa um volume um pouco maior do que de uma colher de sopa cheia (1 mol de água tem aproximadamente 18 mL); Um mol de gás nitrogênio (N₂) inflará um balão com um diâmetro de aproximadamente 30 cm; um mol de açúcar de cana (C₁₂H₂₂O₁₁) tem aproximadamente 340 g. Todas estas quantidades de substâncias citadas, estão contidas em um mol, apresentando aproximadamente 6,022 × 10²³ moléculas.

Entidades do dia-a-dia

Analogias envolvendo o mol são úteis quando se trata de entidades elementares, porém, quando se fala em "entidades do dia-a-dia", tais como laranjas, pãezinhos e até mesmo grãos de areia, as dimensões em volume que atingem um mol destas entidades são extremamente grandes quando comparadas a grandezas corriqueiras de um ser humano. Exemplos:

Ao considerar a espessura de uma folha de papel com cerca de 0,1 mm (10^-4 m), tem-se que um mol de folhas de papel representaria aproximadamente 6,02 × 10¹⁹ m. Sabendo-se que a distância média da Terra à Lua é de 384 000 km (3,84 × 10⁸ m), isso significa dizer que um mol de folhas de papel colocadas umas sobre as outras equivaleria a um comprimento suficiente para ir e voltar da Lua 7,8 × 10¹⁰ vezes, ou seja, cerca de 80 bilhões de vezes;

Supondo que todos os grãos de areia, tenham formato cúbico, com aresta de 1 mm (10^-3 m), pode-se então calcular que seu volume seria de 10^-9 m³. Um mol de grão de areia ocuparia o volume aproximado de 6,02 × 10²³ × 10^-9 = 6,02 × 10¹⁴ m³. Sabendo-se que a área territorial do Brasil é de aproximadamente 8 547 403,5 km² ^[5] = 8,547404 × 10¹² m² , para calcularmos a altura da camada de grãos de areia que cobriria a superfície do país, faz-se: 6,02 x 10¹⁴ m³ / 8,547404 × 10¹² m² = 70,4 m.

Sabe-se que um mol de água ocupa um volume aproximado de 18 mL. Se cada molécula de água assumisse um comprimento de 1 cm e fosse colocada uma seguida da outra, teríamos em um mol 6,02 x 10²¹ m, que seria equivalente à distância de nosso planeta à galáxia da Antena, que foi fotografada pelo telescópio espacial Hubble e dista 63 milhões de anos-luz de nosso planeta. Isso significa que a luz demora 63 milhões de anos para percorrer esta distância.

Referências

↑ IUPAC Compendium of Chemical Terminology, Electronic version, definição de mol. Disponível em: <http://goldbook.iupac.org/M03980.html>. Acesso em: 24 nov. 2007.
↑ * INMETRO Unidades legais de medida. Disponível em: <http://www.inmetro.gov.br/consumidor/unidLegaisMed.asp>. Acesso em: 24 nov. 2007.
↑ CODATA. Volume molar. Disponível em: <http://physics.nist.gov/cgi-bin/cuu/Results?search_for=volume+molar>. Acesso em: 24 nov. 2007.
↑ CODATA. Volume molar do silício. Disponível em: <http://physics.nist.gov/cgi-bin/cuu/Value?mvolsil|search_for=volume+molar>. Acesso em: 24 nov. 2007.
↑ * IBGE Área Territorial Oficial. Disponível em: <http://www.ibge.gov.br/home/geociencias/areaterritorial/historico.shtm>. Acesso em: 24 nov. 2007.

Bibliografia

	INMETRO Unidades legais de medida. Disponível em: <http://www.inmetro.gov.br/consumidor/unidLegaisMed.asp>. Acesso em: 24 nov. 2007.
	IUPAC Compendium of Chemical Terminology, Electronic version, definição de mol. Disponível em: <http://goldbook.iupac.org/M03980.html>. Acesso em: 24 nov. 2007.
	IUPAC. Glossary of terms in quantities and units in clinical chemistry. Pure & Appl. Chem., v. 68, n. 4, p. 957-1000, 1996.
	JENSEN, W. B. The origin of the mole concept. Journal of Chemical Education, Easton, v. 81, n. 10, p. 1409, October 2004. Disponível em: <http://www.jce.divched.org/Journal/Issues/2004/Oct/abs1409.html>. Acesso em: 24 nov. 2007.
	MILLS, Ian; CVITAS, Tomislav; KLAUS, Homann; KALLAY, Nicola; KUCHITSU, Kozo. Quantities, units and symbols in physical chemistry. IUPAC, Blackwell Science Ltda: Oxford, 1993. 2.ed., p. 4. Disponível em: <http://www.iupac.org/publications/books/gbook/index.html>. Acesso em: 24 nov. 2007.
	PERUZZO, T. M.; CANTO, E. L. Mol. In:______. Química: na abordagem do cotidiano. 1. ed. São Paulo: Moderna, 1996. cap. 8, p. 171.
	RUSSELL, J. B. O mol: comentários adicionais. In: ______. Química geral. 2. ed. São Paulo: Makron books e Mcgraw Hill, 1994. v. 1, cap. 2, p. 92-93.
	SILVA, R. R.; ROCHA-FILHO, R. C. Mol - uma nova terminologia. Química Nova na Escola, São Paulo, n. 1, p. 12-14, Mai. 1995. Disponível em: <http://qnesc.sbq.org.br/online/qnesc01/atual.pdf>. Acesso em: 13 abr. 2008.