|

O comportamento dos gases reais parece obedecer
muito bem as leis empíricas dos gases ideais nas
condições ambientais. Isto porque a pressão
atmosférica é baixa. Mas, em condições mais
extremas, de elevadas pressões ou baixas
temperaturas, o comportamento foge muito do previsto
pela lei dos gases ideais.
A causa disso pode ser ao menos uma das 3
propriedades que são exclusivas dos gases reais:
(a) as partículas dos gases reais
têm volume não negligenciável
(b) as forças atrativas e
repulsivas existem e influenciam nos valores de V e
p;
(c) os gases reais podem mudar de
estado físico para uma fase condensada.
 Uma
forma de acompanhar o desvio da idealidade de um gás
real é o parâmetro Z, ou
fator de compressibilidade Z, que é
a razão entre o volume real e o volume que seria
ocupado caso fosse um gás ideal nas mesmas condições
de (T,p), e é definido pela equação abaixo: Uma
forma de acompanhar o desvio da idealidade de um gás
real é o parâmetro Z, ou
fator de compressibilidade Z, que é
a razão entre o volume real e o volume que seria
ocupado caso fosse um gás ideal nas mesmas condições
de (T,p), e é definido pela equação abaixo:
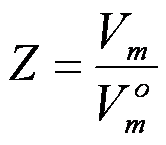
Onde Vm =
Volume molar do gás real e
V°m =
volume molar do gás ideal (ou RT/p).
Se o desvio da idealidade for nulo, então
Vm = V°me
Z=1; se o volume molar do gás real
for menor do que o volume molar do gás ideal, então
Z<1; se Z>1,
significa que o volume real foi maior do que o
ideal.
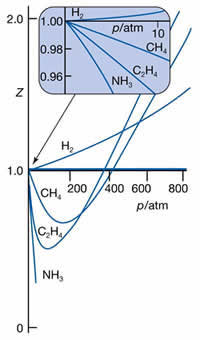
A figura ao lado ilustra
experimentos onde Z
foi medido para vários gases em função da pressão. A
primeira observação, é de que o
valor de Z tende a 1 (para
todos os gases) quando a pressão tende a zero.
Isto é, um gás a baixa pressão tem comportamento
quase ideal. A explicação pode ter origem na teoria
cinética molecular dos gases (KMT): a
baixas pressões, o valor de
l (caminho médio
percorrido por uma molécula antes de uma colisão) é
bastante alto. Isto faz com que o gás atenda
a um dos quisitos da idealidade (espaço entre as
partículas muito maior do que tamanho destas).
|
Forças atrativas e repulsivas
|
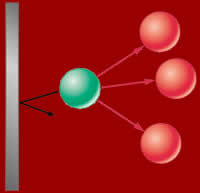 O resultado das forças atrativas (bolas
vermelhas atraem a verde) é de diminuir
tanto a pressão como o volume do gás.
O resultado das forças atrativas (bolas
vermelhas atraem a verde) é de diminuir
tanto a pressão como o volume do gás.
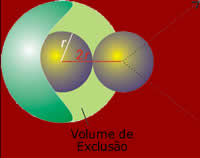
O efeito de que as moléculas do gás real
têm volume e forças repulsivas é de
aumentar a pressão e volume do gás.
|
Outra observação importante:
quando a pressão é bastante alta, todos os gases têm
Z>1, indicando o domínio
das forças repulsivas. De acordo com
a KMT (vide páginas anteriores),com aumento da
pressão, o caminho
l
diminui e a frequência de colisões
z aumenta. As
forças repulsivas forçam o gás a tomar um volume
pouco maior do que aquele esperado para o gás ideal
(onde as forças repulsivas não existem).
Já em pressões
intermediárias, o valor de Z<1 indica que o
domínio é das forças atrativas. A
atração mútua exercida pelas moléculas fazem o
volume "encolher", ficando menor em comparação ao
volume ideal.
|
Situação Ideal
|
Situação não-Ideal
|

>pressão baixa
>temperatura alta |

>alta pressão
>temperatura baixa |
 |
Outra propriedade dos gases reais é a capacidade de
se condensarem, para formar um líquido ou um sólido.
O aumento da pressão ou a
diminuição da temperatura pode provocar a
condensação do gás.
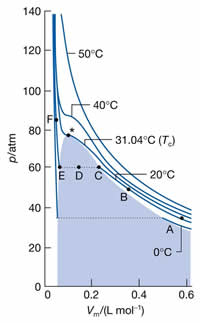
A figura ao lado ilustra
experimentos onde o volume foi medido
para pressões diferentes do gás CO2,
em várias temperaturas. As isotermas de
temperatura elevada em muito se assemelham às
isotermas de Boyle. Mas a medida em que a
temperatura é diminuida, um fato muito estranho
acontece: A isoterma de 20°C,
mostra que, do ponto C até o ponto E, a diminuição
de volume ocorre sem nenhum aumento da pressão;
isto porque o gás está se
condensando. Como o líquido é muito
mais denso, o volume diminui. Após o ponto E,
qualquer diminuição do volume requer quantidade
infinita de pressão; a compressibilidade do líquido
é muito baixa.
Mas na temperatura de 31,04°C,
a condensação deixa de existir e o gás não pode ser
mais liquefeito pelo simples aumento da pressão.
Esta é a Temperatura Crítica ( Tc ) do
gás. A partir desta temperatura, o
gás não pode ser liquefeito e é chamado de gás
permanente.

Acima da temperatura crítica,
o gás não pode ser mais liquefeito. Como
nesta temperatura o gás tem propriedades distintas,
é chamado de fluído
supercrítico. É o que vemos na
terceira fotografia do conjunto acima: a interface
líquido-vapor desapareceu. Atualmente,
os fluídos supercríticos são muito
empregados na indústria química. O
CO2 supercrítico, por exemplo, é usado na
extração da cafeína para o preparo
do café descafeinado.
Descobertos os devios da
idealidade, muitos foram os físcos,
matemáticos e físico-químicos que tentaram descrever
uma nova equação de estado para gases reais. A mais
elegante e famosa delas, sem dúvida, é a
Equação de Estado dos Gases Reais de van der Waals.
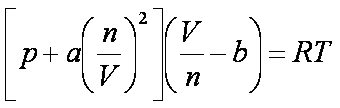
 Johannes
D. van der Waals propôs uma
modificação da lei geral dos gases, levando em conta
o tamanho das partículas e as
interações intermoleculares. Johannes
D. van der Waals propôs uma
modificação da lei geral dos gases, levando em conta
o tamanho das partículas e as
interações intermoleculares.
Esta equação foi proposta em sua tese de doutorado,
em 1873. Basicamente, apenas
duas correções foram feitas: o termo
+a(n/V)1/2
corrige a diminuição da pressão devido a forças
atrativas, enquanto que o termo -b
corrige o volume devido ao tamanho das moléculas do
gás real.
Os termos a e b
são chamados coeficientes de van der Waals,
e são determinados experimentalmente pelo ajuste de
isotermas de van der Waals com dados experimentais.
A tabela abaixo apresenta os
valores dos coeficientes de van der Waals para
alguns gases.
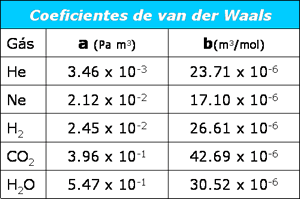
Acima dissemos que o coeficiente
a está associado às
forças intermoleculares presentes no gás real.
Compare os valores de a
dos gases He e H2O.
O coeficiente a da
água é mais de 100 vezes maior do que o do hélio.
Isto indica uma interação intermolecular muito mais
forte nas moléculas de H2O
do que nos átomos de He. Da mesma forma, se
compararmos o coeficiente
b CO2
e H2, veremos que o
b é maior para o
gás carbônico, que obviamente possui uma molécula
também maior. Como falamos anteriormente, o
b está
relacionado ao tamanho das moléculas.
  |
A equação de van der Waals é magnífica não somente
por sua simplicidade, mas também pela capacidade de
prever o comportamento dos gases reais com
fidelidade, prevendo até mesmo o fenômeno da
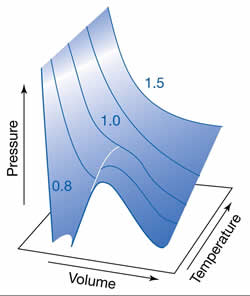
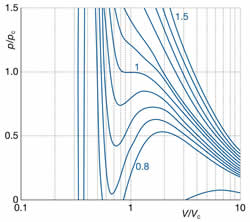
condensação e a temperatura crítica. Quando
isotermas p x V são traçadas pela
equação de van der Waals (vide
figuras acima), surgem ondulações
nas curvas nas temperaturas inferiores à temperatura
crítica. Estas ondulações são irreais, e representam
o equilíbrio líquido - vapor
que se estabelece nestas condições de p e
T. Normalmente, são substituidas por linhas retas de
acordo com a construção matemática de Maxwell.
A equação de van der Waals pode ser expressa em
termos de Volume molar (V/n), resultando na seguinte
expressão:
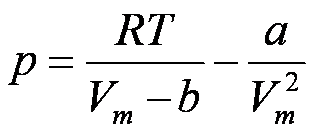 Perceba alguns significados desta equação:
Perceba alguns significados desta equação:
(a) Em T
elevada e Vm
grande, as isotermas de vdW coincidem com as
isotermas do gás perfeito.
Quando T é
alta, RT é
muito grande se comparado ao valor do segundo termo
da equação de vdW; se o Vm for grande,
Vm
>> b
no primeiro termo.
(b) Os líquidos e os gases coexistem quando
os efeitos de coesão e os de dispersão estão
equilibrados. As ondulações ocorrem quando
os dois termos da equação tem grandezas semelhantes.
O primeiro provém da energia cinética
e interações repulsivas; o
segundo representa o efeito das interações
atrativas.
(c) As coordenadas críticas podem ser
obtidas através das constantes de van der Waals.
As isotermas oscilam quando T<Tc; quando
T~Tc elas convergem e em T=Tc a curva tem uma
inflexão típica, com primeira e segunda derivadas
nulas. As coordenadas podem ser calculadas através
destas derivadas.
Assim, terminamos esta etapa da aula
sobre o estado gasoso. A seguir, elaboramos um
rápido exame para você testar seu aprendizado. Para
seguir, use a barra de navegação no topo da página.
|