|
 Uma
das funções da Físico-Química é a de, baseada em
observações experimentais, desenvolver
modelos teóricos que justifiquem estas
observações. Além de explicar fatos conhecidos, tais
modelos devem prever o comportamento do
sistema em situações diferentes, passíveis
de comprovação experimental. É o que faz o modelo
cinético dos gases, também conhecido como
Teoria Cinética Molecular dos Gases (KMT). Uma
das funções da Físico-Química é a de, baseada em
observações experimentais, desenvolver
modelos teóricos que justifiquem estas
observações. Além de explicar fatos conhecidos, tais
modelos devem prever o comportamento do
sistema em situações diferentes, passíveis
de comprovação experimental. É o que faz o modelo
cinético dos gases, também conhecido como
Teoria Cinética Molecular dos Gases (KMT).
Até então, vimos propriedades dos gases sempre com
enfoque macroscópico. A KMT surgiu
no final do século XIX, quando a teoria
atômica já estava bem difundida. E este
modelo tenta explicar o
comportamento macroscópico dos gases com base nas
propriedades microscópicas da matéria.
Em outras palavras, o modelo caracteriza, a partir
das propriedades individuais das partículas que
compões o gás, o comportamento esperado para uma
grande quantidade deste.
Como vimos anteriormente, este modelo assume que
(I) um
gás é feito por partículas que estão em constante
movimento aleatório;
(II) o tamanho das partículas é
negligenciável se comparado à distância entre elas;
(III) não
há forças atrativas ou repulsivas entre as
partículas ou mesmo entre estas e as paredes do vaso
que as contém; (IV)
as colisões entre as partículas são
perfeitamente elásticas;
(V) a energia total de
uma amostra de gás é igual à soma das energias
cinéticas individuais de cada partícula presente e a
energia cinética média das partículas é proporcional
à temperatura do gás.
Vamos ilustrar como o modelo define algumas
propriedades macroscópicas dos gases que já
conhecemos:
|
c,
avelocidade média do gás
|
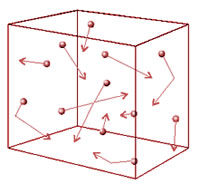
Numa amostra de gás, as moléculas se movem
em sentidos e velocidades aleatórias. Por
isso, a velocidade média precisa se definida
como a média dos módulos das velocidades
individuais, ou a raiz quadrada do somatório
dos quadrados das velocidades de cada uma
das moléculas dividida pelo número de
moléculas, tal como mostra a equação abaixo:
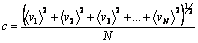
Desta forma, a energia cinética média das
partículas é dada por:
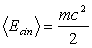 |
A hipótese de que as forças atrativas e repulsivas
são nulas implica que a energia potencial
das moléculas (a energia devida a suas
posições) independe da separação entre estas e,
portanto, pode ser considerada nula.
Por isso, a energia de uma amostra de gás é
simplesmente a soma das energias cinéticas de cada
uma das partículas. Então, quanto mais rápido se
moverem as partículas, maior será a energia total do
gás. Ocorre que a velocidade média das partículas
(veremos a seguir) é diretamente proporcional à
temperatura da amostra. Portanto, podemos concluir:
um aumento de temperatura
provoca um aumento na velocidade média das
partículas e, consequentemente, um aumento na
energia do gás. Logo, a energia de
um gás é proporcional a sua temperatura.
Uma outra forma de ver esta relação é seguinte: para
a KMT, a temperatura de um
gás é, na verdade, uma escala que indica a
velocidade média das moléculas presentes na amostra.
Isto significa que se dois gases estão
em equilíbrio térmico, a energia cinética média de
ambos é também igual. Veremos adiante
que isto é a causa das diferenças nas velocidades de
efusão e difusão dos gases.
 Em
uma amostra de gás a uma determinada temperatura,
sempre há moléculas muito rápidas e também moléculas
muito lentas, pois o movimento é aleatório.
O modelo cinético prevê uma
curva de distribuição de velocidades das partículas
em função da temperatura. Em
uma amostra de gás a uma determinada temperatura,
sempre há moléculas muito rápidas e também moléculas
muito lentas, pois o movimento é aleatório.
O modelo cinético prevê uma
curva de distribuição de velocidades das partículas
em função da temperatura.
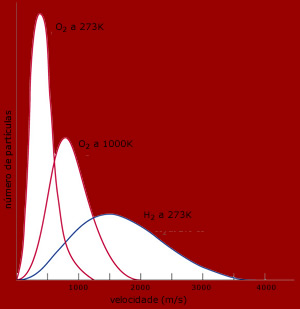
A figura ao lado trás 3 curvas de
distribuição de velocidades. As duas
primeiras são da mesma substância, em duas
temperaturas diferentes. Repare que quando a
temperatura aumenta, a velocidade média do oxigênio
aumenta também. Entretanto, há sempre
moléculas lentas, mesmo em temperaturas elevadas.
Outra constatação surge quando comparamos as curvas
para dois gases diferentes na mesma temperatura.
O gás hidrogênio apresenta uma distribuição
indicando velocidade média maior do que a do gás
oxigênio. Isto porque a massa molar do
hidrogênio é menor.
Para o modelo cinético dos gases,
a pressão é fruto das colisões das moléculas
do gás contra as paredes do recipiente.
Cada colisão dá uma pequena força contra a parede do
recipiente; mas, como ocorrem bilhões de colisões a
cada segundo, as paredes experimentam uma força
constante, resultando em uma pressão estável do gás.
De acordo com este modelo, a pressão pode ser
descrita da seguinte maneira:
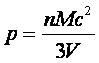
Esta equação se assemelha à equação dos gases, pois
podemos expressá-la como pV=nMc2/3.
Desta maneira, como sabemos que pV=nRT, podemos
dizer que nRT = nMc2/3.
Com isso, obtemos uma expressão para a
velocidade média c:
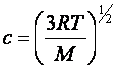
Esta expressão nos diz que a
velocidade média c é proporcional à raiz quadrada da
temperatura, e c diminui com o
aumento da massa molar. Isto ocorre na mesma razão
(M)1/2 que o observado empiricamente por
Graham.
|
Efusão e Difusão de Gases |
 No experimento acima, ocorre algo
bizarro: após a abertura da válvula, o
balão murcho fica ainda mais murcho e o
balão cheio ainda mais cheio. Isto é uma
consequência da lei de Graham: ocorre
porque o gás do balão azul é o hélio, de
menor massa molar que o gás do balão
vermelho, o nitrogênio. Logo, a
velocidade de efusão do gás do balão
azul através da válvula é maior do que a
do gás do balão vermelho.
No experimento acima, ocorre algo
bizarro: após a abertura da válvula, o
balão murcho fica ainda mais murcho e o
balão cheio ainda mais cheio. Isto é uma
consequência da lei de Graham: ocorre
porque o gás do balão azul é o hélio, de
menor massa molar que o gás do balão
vermelho, o nitrogênio. Logo, a
velocidade de efusão do gás do balão
azul através da válvula é maior do que a
do gás do balão vermelho.
|
A observação empírica feita por Graham dizia que
a velocidade de difusão
(passagem do gás para outro meio) ou efusão
(passagem do gás por um orifício ou barreira) de um
gás era inversamente proporcional ao quadrado de sua
massa molar. Ou seja, quanto mais
pesado for o gás, menor sua velocidade de efusão. O
modelo cinético chega quantitavamente ao mesmo
resultado.
Anteriormente, falamos que se dois gases estão em
equilíbrio térmico, suas energias cinéticas médias
sao iguais. Então, vamos comparar as velocidades de
efusão de dois gases na mesma temperatura, o gás (A)
e o gás (B).
Com base na definição de energia cinética no quadro
acima, temos que
m(A).c(A)2 = m(B).c(B)2
Portanto, a relação entre as velocidades de A/B pode
ser dada por
c(A)/c(B) = (m(B)/m(A))1/2
Isto é, se a massa molar de B for maior do que a
massa molar de A, a velocidade de A será maior
(razão maior do que 1) do que a velocidade de B.
|
l
e
z : Colisões Moleculares |
Como falamos anteriormente, o modelo cinético afirma
que as moléculas do gás colidem (elasticamente) com
outras e com as paredes do recipiente. Veremos agora
que o modelo oferece ferramentas quantitativas para
avaliar as colisões, através de parâmetros como
o caminho médio percorrido pelas moléculas
até uma colisão (
l ), a frequência de
colisões (
z
) e o intervalo médio de tempo entre duas
colisões (1/z).
De acordo com a KMT, o caminho livre e a frequência
de colisões são definidos como:
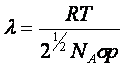 .................
.................
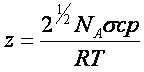 |
Onde s é a seção
transversal de choque da molécula (pd2).
De acordo com estas equações, podemos perceber que:
a) l
é inversamente proporcional a p:
quanto maior a pressão, menor é a distância
percorrida por uma molécula antes da colisão;
b) l
é inversamente proporcional a
s:
moléculas menores percorrem distâncias maiores antes
da colisão;
c) z é proporcional a
p: em um gás pressurizado, a
frequência de choques é maior.
Outra observação: para um gás real ter comportamento
de gás perfeito (ou ideal) é necessário um requisito
básico: l
>> s.
Desta maneira, o espaço entre as partículas é muito
maior do que o tamanho das mesmas.
A seguir, nossa aula prossegue com os gases reais.
Veremos que alguns ajustes são necessários às
equações que conhecemos para que elas funcionem com
todos os gases em todas as condições. E estudaremos
os desvios da idealidade apresentados por alguns
gases. Para seguir adiante, use a barra de navegação
no topo da página.
|