GASES
1. Transformações Gasosas
1.1. Introdução
Todo gás é constituído de partículas (moléculas) que estão em contínuo movimento desordenado. Esse movimento de um grande número de moléculas provoca colisões entre elas e, por isso, sua trajetória não é retilínea num espaço apreciável, mas sim caminham em ziguezague. Essas colisões podem ser consideradas perfeitamente elásticas.
O estado em que se apresenta um gás, sob o ponto de vista microscópico, é caracterizado por três variáveis: pressão, volume e temperatura. São denominadas variáveis de estado.
I. Volume
O volume de qualquer substância é o espaço ocupado por esta substância. No caso dos gases, o volume de uma dada amostra é igual ao volume do recipiente que a contém.
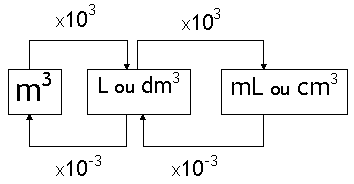
As unidades usuais de volume são: litro (L), mililitro (mL), metro cúbico (m3), decímetro cúbico (dm3) e centímetro cúbico (cm3).
II. Temperatura
É a medida do grau de agitação térmica das partículas que constituem uma substância.
No estudo dos gases, é utilizada a escala absoluta ou Kelvin (K) e, no Brasil, a escala usual é a Celsius ou centígrada (°C). Portanto, para transformar graus Celsius (t) em Kelvin, temos:
III. Pressão
A pressão é definida como força por unidade de área. No estado gasoso, a pressão é o resultado do choque de suas moléculas contra as paredes do recipiente que as contém.
A medida da pressão de um gás é feita através de um aparelho chamado manômetro.
O manômetro é utilizado na medida da pressão dos gases, dentro de recipientes fechados. É formado por um tubo em U, contendo mercúrio.
Encontramos dois tipos de manômetro:
1. Com extremidade aberta
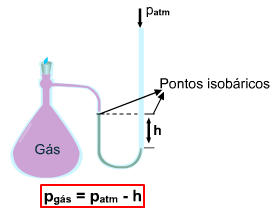
2. Com extremidade fechada
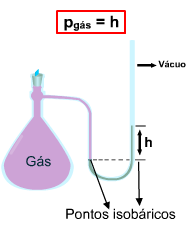
As unidades de pressão usuais são:
atmosfera (atm), centímetros de mercúrio (cmHg), milímetros de mercúrio (mmHg);
Torricelli (torr).
1 atm = 76 cmHg = 760 mmHg
1 mmHg = 1 torr
1.2. Leis Físicas dos Gases
Uma dada massa de gás sofre uma transformação quando ocorrem variações nas suas variáveis de estado. Começamos o estudo modificando-se apenas duas das grandezas e a outra se mantém constante.
I. Lei de Boyle-Mariotte
“À temperatura constante, uma determinada massa de gás ocupa um volume inversamente proporcional à pressão exercida sobre ele”.
Esta transformação gasosa, onde a temperatura é mantida constante, é chamada de transformação isotérmica.
Experiência da Lei de Boyle-Mariotte
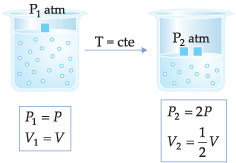
A lei de Boyle-Mariotte pode ser representada por um gráfico pressão-volume. Neste gráfico, as abscissas representam a pressão de um gás, e as ordenadas, o volume ocupado.
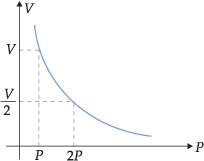
A curva obtida é uma hipérbole, cuja equação representativa é PV = constante. Portanto, podemos representar:
II. Lei de Charles/Gay-Lussac
“À pressão constante, o volume ocupado por uma massa fixa de gás é diretamente proporcional à temperatura absoluta."
Esta transformação gasosa, onde a pressão é mantida constante, é chamada de transformação isobárica.
As relações entre volume e temperatura podem ser representadas pelo esquema:
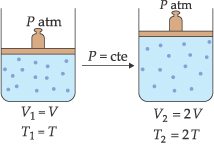
Graficamente, encontramos:
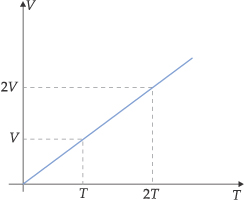
A reta obtida é representada pela equação:
V = (constante) · T ou V/T = constante
Com isso, ficamos com:
III. Lei de Charles/Gay-Lussac
“A volume constante, a pressão exercida por uma determinada massa fixa de gás é diretamente proporcional à temperatura absoluta.”
Esta transformação gasosa, onde o volume é mantido constante, é denominada de transformação isocórica, isométrica ou isovolumétrica.
As relações entre pressão e temperatura são representadas a seguir:
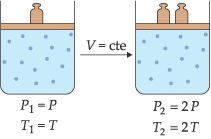
Graficamente, encontramos:
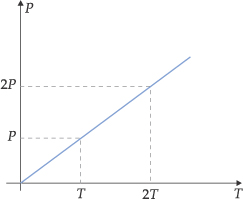
A reta obtida é representada pela equação:
P = (constante) · T ou P/T = constante
Com isso, ficamos com:
1.3. Gás Perfeito ou Ideal
Obedece rigorosamente às Leis Físicas dos Gases em quaisquer condições de temperatura e pressão.
1.4. Gás Real
Não segue o comportamento do gás ideal, principalmente em pressões muito altas e/ou em temperaturas baixas, porque ocorre alta redução de volume e as partículas, muito próximas, passam a interferir umas no movimento das outras.
Um gás real aproxima-se do comportamento de um gás ideal à medida que diminui a pressão e aumenta a temperatura.
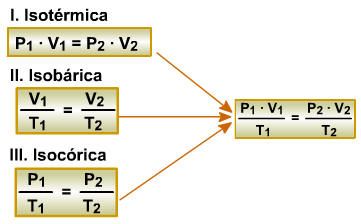
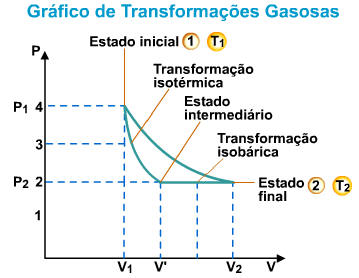
2. Equação Geral dos Gases
Esta equação é utilizada quando ocorre transformação gasosa em que as três variáveis de estado (P, V e T) se modificam simultaneamente.
Ela é obtida por meio da relação matemática entre as transformações gasosas estudadas anteriormente.
3. Condições Normais de Temperatura e Pressão (CNTP, CN ou TPN)
São definidas como condições normais de temperatura e pressão quando o gás é submetido a uma pressão de 1 atm e à temperatura de 0 °C. Portanto, podemos colocar:
P = 1 atm = 760 mmHg
T = 0 °C = 273 K
4. Lei de Avogadro
“Volumes iguais de gases quaisquer, à mesma temperatura e pressão, encerram o mesmo número de moléculas."
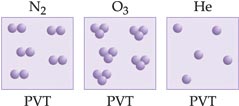
Sendo n a quantidade em mols de cada gás, podemos concluir:
Determinou-se experimentalmente o volume ocupado por 1 mol de qualquer gás nas CNTP e foi encontrado o valor aproximadamente igual a 22,4 L. Portanto, podemos dizer que:
6. Equação de Clapeyron
As leis de Boyle e Charles/Gay-Lussac podem ser combinadas com a lei de Avogadro para relacionar volume, pressão, temperatura e quantidade em mols de um gás.
Tal relação é chamada de equação de estado de um gás. Ela pode ser encontrada das seguintes formas:
I. Lei de Boyle-Mariotte
V é proporcional a
quando T e n são constantes.
II. Lei de Charles/Gay-Lussac
V é proporcional a T onde P e n são constantes.
P é proporcional a T onde V e n são constantes.
III. Lei de Avogadro
V é proporcional a n quando T e P são constantes. Agrupando as quatro expressões encontramos:
V é proporcional a
· (T) · (n) ou
V = R ·
· (T) · (n), onde R representa a constante de proporcionalidade e
é chamada de constante universal dos gases. A equação de estado pode então
ser representada por:
P · V = n ·R · T
Esta equação também é denominada de equação de Clapeyron, em homenagem ao físico francês que a determinou.
A constante R pode assumir vários valores dentre os quais destacamos:
Saiba Mais...
Lei dos Gases Ideais causa queda de um LearJet
A lei dos gases ideais, PV=nRT, diz que o número de moléculas de gás em um determinado volume é proporcional à pressão do gás. No dia 25 de outubro de 1999, um LearJet caiu em Mina, South Dakota, USA. A causa do acidente foi a depressurização da cabine. O avião estava a 10 mil pés de altura (~3 km). Nesta altitude, a pressão atmosférica é menor e, consequentemente, o ar é menos denso, mais rarefeito. Dentro do avião, que deve ser selado, a pressão é controlada pelo bombeamento de oxigênio. Durante o vôo, houve uma depressurização - todos os passageiros e tripulação rapidamente ficaram inconscientes e, provavelmente, mortos, por falta de oxigênio: menor P resulta em menor n. Por mais de 3 horas voaram nesta situação, guiados pelo piloto automático. Uma das evidências de que a depressurização, de fato, ocorreu, era de que as janelas do avião estavam cobertas de gelo. A 10 mil pés, o avião pode ser encarado como um grande cilindro de ar comprimido. Se estiver vazando, o ar estará sofrendo uma expansão. PV=nRT diz que este é um processo endotérmico e, portanto, retira calor das vizinhanças - levando até mesmo ao congelamento do vapor de água!
A perda de consciência é tão rápida porque o sangue perde oxigênio com se estivesse em ebulição. As células cerebrais ficam sem oxigênio e morrem em poucos minutos.
7. Densidade dos Gases
A densidade gasosa pode ser trabalhada sob duas formas: a densidade absoluta e a densidade relativa.
7.1. Densidade Absoluta
A densidade absoluta é uma relação entre a massa e o volume ocupado por um gás, em determinadas condições de temperatura e pressão.
Esta densidade pode ser encontrada, levando-se em consideração a pressão e a temperatura absoluta, partindo-se da equação de estado do gás ideal:
P · V = n · R · T
Sabendo que: d = m/V
P · M = d · R · T
A unidade utilizada é o g/L.
Trabalhando-se nas CNTP (P = 1 atm e T = 273 K), encontramos a seguinte equação:
7.2. Densidade Relativa
A densidade relativa é encontrada através da relação entre as densidades absolutas de dois gases, medidas nas mesmas condições de temperatura e pressão.
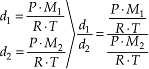
Esta relação indica quantas vezes um gás é mais denso ou menos denso que outro gás. Por exemplo, uma bexiga com gás hidrogênio mantém-se suspensa no ar porque o gás hidrogênio é menos denso que o ar.
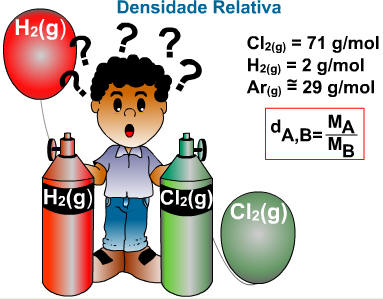
8. Mistura Gasosa
A mistura entre dois ou mais gases sempre constitui um sistema homogêneo.
Consideremos inicialmente dois recipientes contendo, o primeiro, gás nitrogênio (N2) e o segundo, gás hélio (He).
Os dois gases são misturados em um terceiro recipiente, conforme o esquema representado abaixo.
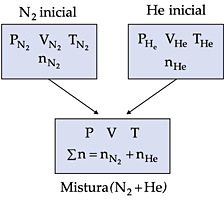
Para a mistura gasosa, é possível estabelecermos as seguintes relações:
8.1. Equação de Estado
P · V =
n
· R · T
onde:
Não esquecer que
, portanto a mistura apresentada fica:
Para uma mistura gasosa qualquer, a quantidade em mols fica:
n = n1 + n2 + n3 + ...
8.2. Equação Geral dos gases
Partindo de:
e sabendo que;
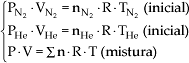
A soma das quantidades em mols fica:
Podemos representar a equação geral para mistura gasosa:
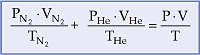
Para a equação representada, utilizamos a mistura de dois gases, portanto, para uma mistura qualquer, contendo mais de dois gases, a equação fica assim representada:
onde P1, V1,T1,P2,V2,T2 , … representam a situação inicial de cada gás.
8.3 Pressão Parcial
Utilizando o mesmo esquema do módulo anterior, temos:
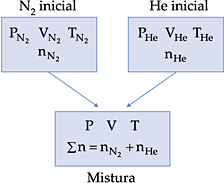
A pressão da mistura gasosa (P) corresponde à soma das pressões exercidas pelo hélio e pelo nitrogênio dentro do recipiente. A pressão que cada gás exerce na mistura gasosa é chamada de pressão parcial. Portanto, podemos enunciar a lei de Dalton (das pressões parciais) que diz: a pressão total corresponde à soma das pressões parciais dos gases componentes da mistura gasosa.
P = pHe + pN2
Para o cálculo da pressão parcial podemos utilizar:
a) Equação de estado
pN2 · V = nN2 · R · T e pHe · V = nHe · R · T
onde V e T são da mistura gasosa.
b) Equação geral
Como a quantidade em mols de cada gás não varia, podemos escrever:
Utilizando a equação de estado, temos:
Inicial
mistura
Estabelecendo a igualdade:
Para o hélio, a equação fica:
c) Relação entre pressão da mistura gasosa e pressão parcial
Inicialmente, definimos uma forma de concentração, denominada de fração molar (x).
A fração molar corresponde a razão entre a quantidade em mols do gás presente na mistura e a quantidade total, em mols, de gás. Portanto, a equação fica:
Para estabelecer a relação entre as pressões, recorremos à equação de estado:
pHe · V = nHe · R · T (pressão parcial)
P · V =
n
· R · T (mistura gasosa)
Dividindo uma equação pela outra:
encontramos:
ou
Para o nitrogênio: PN2 = P · xN2
9. Efusão e Difusão Gasosa
Considerando que um recipiente contenha gás, se seu
cheiro se espalhar todos que estarão ao redor, iram sentir o cheiro forte do
gás (fato muito conhecido). Esse fato ocorre, pois as moléculas de um gás se
movimentam com facilidade através dos espaços vazios entre as moléculas,
fazendo com que elas se misturem uniformemente com eles.
Podemos pensar também que essas moléculas podem atravessar as paredes
porosas, porém nem todas na mesma velocidade, independente se os gases estão
ou não nas mesmas condições de temperatura e pressão.
Difusão gasosa – é a forma na
qual, os gases atravessam uma parede porosa, e nesse mesmo processo se
misturam de maneira uniforme com outros gases.
Porém, a efusão gasosa é
conceituada como uma forma em que um gás escapa de um recipiente, por meio
de um pequeno furo, para o vácuo.
Thomas Graham foi um químico britânico, que estudou a efusão gasosa, ele
criou a lei que o explica.
“As velocidades de efusão dos gases são inversamente proporcionais às
raízes quadradas de suas massas específicas, quando submetidos à mesma
pressão e temperatura.”
Este site foi atualizado em 04/03/19