|
Quando se estuda uma determinada reação química, três questões são
importantes:
1. A reação avança
naturalmente na direção de formação dos produtos?
2. O sistema
reacional terá quantidade suficiente de produtos ao atingir o
equilíbrio?
3. Se isto
acontecer, qual é a rapidez do processo?
Ao se estudar Cinética Química, focaliza-se na terceira questão. Ao
se estudar Equilíbrio Químico, aborda-se a segunda questão. A
Termodinâmica Química investiga a primeira questão.
Para que um processo possa ser observado de forma significativa, os
três aspectos anteriormente levantados devem ser favoráveis.
Exemplo:
H2 (g) + ½ O2
(g) → H2O(ℓ)
— este processo é termodinamicamente viável
— este processo, à temperatura ambiente, ocorre muitíssimo
lentamente
Conclusão: uma
mistura de H2 e
O2 é estável à
temperatura ambiente
A termodinâmica diz respeito às transferências de calor ou outras
formas de energia, que estão envolvidas em processos físicos e
químicos.
Aplicada à Química, a termodinâmica permite prever se uma
transformação química é possível, ou impossível, em determinadas
condições experimentais, ou seja, se o processo é espontâneo ou não
nas condições em questão.
A termodinâmica se baseia em leis de natureza experimental,
independentes de qualquer modelo que leve em conta a estrutura
microscópica da matéria.
Antes de avançar, deve-se revisar alguns conceitos.
Conceitos Básicos
|
|
Sistema -
porção particular do universo cujas propriedades se deseja
estudar, os sistemas podem ser:
a) Sistema
Isolado: não troca matéria nem energia com a vizinhança,
não varia de volume.
b) Sistema
Fechado: pode trocar energia com a vizinhança e variar
de volume, mas não troca matéria.
c) Sistema
Aberto: pode trocar matéria e energia com a vizinhança.
Vizinhança (ou ambiente) –
todas as demais partes do universo que não fazem parte do
sistema.
Estado –
situação de equilíbrio em que as propriedades macroscópicas
do sistema como: temperatura, pressão, densidade, composição
química, volume, estado físico (sól., líq., gás.), forma
cristalina, são bem definidas e não se alteram com o tempo.
Funções de Estado –
propriedade do sistema caracterizada por um valor numérico
bem definido para cada Estado e independente da maneira pela
qual o estado é alcançado.
Pressão (P), temperatura (T), e volume (V).são
Funções de Estado. Outras Funções de Estado importantes para
o estudo da termodinâmica são: energia interna (E ou U),
entalpia (H), entropia (S) e energia livre
de Gibbs (G).
As Funções de Estado tem duas propriedades importantes:
a) Quando um sistema sofre uma transformação, as alterações
das funções de estado somente dependem do estado inicial e
do estado final, ou seja, não dependem do caminho da
transformação.
b) As funções de estado são inter-relacionadas através de
equações de estado, atribuindo-se valores para algumas,
pode-se definir os valores de outras.
Exemplo:
|
PV = nRT
H = U + PV
ou H = E + PV
G = H – TS |
Propriedades Intensivas –
não dependem da quantidade ou tamanho do sistema, em
sistemas homogêneos, as propriedades intensivas são
idênticas em toda a extensão do sistema, mas em sistemas
heterogêneos estas propriedades variam nas diferentes fases.
Exemplo: pressão (P), temperatura (T),
densidade (d), fração molar (),
cor.
Propriedades Extensivas –
dependem da quantidade ou tamanho do sistema.
Exemplo: volume (V), energia (E), massa (m),
n° de mols (n). |
|
Propriedades
Intensivas e Extensivas |
|
Propriedades Intensivas: São
propriedades que não dependem da dimensão da amostra de
substância.
Propriedades Extensivas: São
propriedades que dependem da dimensão da amostra de
substância.
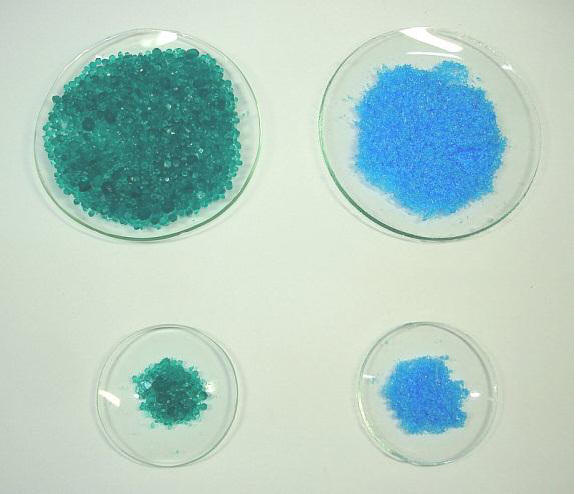
Agora que
definimos as
propriedades intensivas e extensivas,
exercitemos estes conceitos observando a foto
abaixo. Nela estão representadas diferentes
quantidades de sulfato de níquel heptahidratado
(verde) e sulfato de cobre pentahidratado (azul)
A partir da foto abaixo, marque
no quadro as propriedades intensivas e
extensivas possíveis de se observar, quando não
for possível, marque a opção correspondente.
|
 |
|
Transformações
Termodinâmicas
|
|
As transformações termodinâmicas são classificadas em:
- Transformações Reversíveis
- Transformações Irreversíveis,
Seja uma variável qualquer que caracterize um estado A de
um sistema. Esta variável é alterada por uma transformação a
um estado C,
passando por um estado intermediário B.
Se existe uma transformação, que conduz o estado C de
volta para o estado A,
pelo mesmo caminho (passando pelo estado intermediário B),
diz-se que a Transformação
é Reversível.
Todas as transformações que não obedecem esta regra são Transformações
Irreversíveis.
Exemplo:
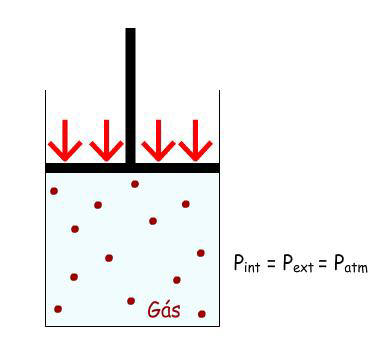
Dispõe-se de um gás dentro de um cilindro e o seu volume (V1)
é limitado por um pistão. APinterna = P externa = P atmosférica.
 |
Este volume V1 pode
ser reduzido a um volume V2 por
aumento da pressão sobre o pistão.
Pode-se realizar esta transformação por diversos caminhos,
sendo dois destes citados abaixo:
1°- Colocar
um bloco de massa “m” sobre o pistão, de forma que
o volume diminua bruscamente de V1 para V2.
A transformação foi brusca, pois a pressão aumentou
bruscamente de um valor igual a Patm (P1)
até um valor P2,
que corresponde ao peso do bloco dividido pela área do
pistão, o que provoca variação brusca de volume.
Graficamente, esta transformação pode ser representada por:
Para retornar ao estado inicial, basta retirar o bloco de
massa m de
cima do pistão. Desta forma, a pressão é diminuída
bruscamente de P2 para P1 e
o volume aumentado de V2 paraV1.
Pode-se observar que o caminho
de retorno da
transformação, não
foi o mesmocaminho da transformação direta, ou
seja, não foi possível retornar ao estado inicial pelo mesmo
caminho – Transformação
Irreversível.
2° -
Colocar sobre o pistão um punhado de areia com massa “m”
igual à massa do bloco anterior. Mas este punhado de areia
deve ser colocado grão a grão, de forma a provocar um
aumento infinitesimal de pressão a cada grão adicionado, e
conseqüentemente levar a uma diminuição infinitesimal de
volume.
Após a adição de todos os grãos de areia, os quais
provocaram uma sucessão de transformações infinitesimais, a
pressão P2 e
o volume V2 são
atingidos. A transformação foi gradual e muito lenta.
Graficamente, esta transformação pode ser representada como
uma isoterma, se T permanecer constante durante a
transformação.
OBS: Como cada etapa de compressão é infinitesimal pode-se
representar a sucessão de pequenos “degraus” sobre a
isoterma, como a própria isoterma.
Para se retornar ao estado inicial, é preciso remover os
grãos de areia. Se estes grãos forem removidos um por um,
cada grão removido provoca uma redução infinitesimal na
pressão, o que acarreta um aumento infinitesimal de volume.
Após a remoção de todos os grãos, os quais provocaram uma
sucessão de transformações infinitesimais, o sistema retorna
gradual e lentamente ao estado inicial.
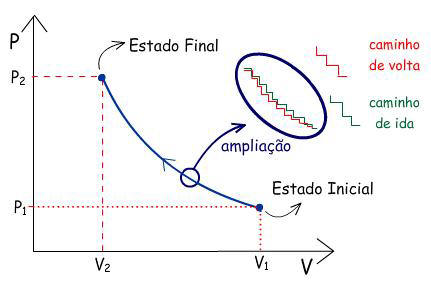 |
Pode-se observar que o caminho de retorno desta
transformação foi o mesmo da transformação direta, desta
forma, ocorreu uma Transformação
Reversível, pois o retorno ao estado inicial
ocorreu pelo mesmo caminho da transformação direta.
Num Processo
Reversível as
Funções de Estado do sistema e da vizinhança nunca diferem
entre si mais do que uma quantidade infinitesimal em cada
passo da transformação:
P externa = P interna ±
dP
Onde: dP -
variação infinitesimal de P
Como não existe mais do que uma diferença infinitesimal
entre as Funções de Estado do sistema e da vizinhança, estas
transformações ocorrem numa velocidade infinitamente lenta e
são ditas transformações quase estáticas.
A direção de uma transformação reversível pode ser alterada
em qualquer momento, simplesmente fazendo uma modificação
infinitesimal na vizinhança.
Exemplo:
Uma compressão reversível pode ser transformada em uma
expansão reversível, diminuindo-se a Pexterna
por um infinitésimo (retirada de um grão de areia).
Por outro lado, uma transformação irreversível ocorre a uma
velocidade finita. As propriedades do sistema e da
vizinhança diferem por quantidades finitas. Logo, estas
transformações não podem ser invertidas fazendo modificações
infinitesimais na vizinhança, ou seja, é preciso uma
modificação brusca na vizinhança para inverter o processo.
OBS: Não existe na natureza um processo que seja
rigorosamente reversível. |
| |
Calor e Trabalho – Primeiro Princípio da Termodinâmica
Conservação da Energia
|
|
A termodinâmica é descrita em função de três Leis (ou
Princípios). O Primeiro Princípio da Termodinâmica é o “Princípio
da Conservação da Energia”.
Para enunciar o primeiro princípio, é preciso entender o
conceito de Energia
Interna (E)de um sistema e a maneira de
alterar esta Energia Interna.
A Energia Interna (E) é a soma da energia Cinética
e Potencial das partículas que constituem o sistema:
- A Energia Cinética inclui a energia dos movimentos
(translação, rotação, vibração) dos elétrons, átomos e
moléculas.
- A Energia Potencial é o resultado das ligações químicas
entre os átomos e das atrações intermoleculares.
A Energia Interna é uma Função
de Estado, ou seja, uma propriedade que só depende
do Estado em que se encontra o sistema no momento, e não
depende da história do sistema.
Quando o sistema passa de um estado para o outro, sua
energia interna varia de um valor bem definido:
∆E = E final – E inicial
Normalmente, se tem interesse nas variações de Energia
Interna e não nos seus valores absolutos em cada Estado.
Essas variações podem ser medidas quantificando as trocas de
energia entre o sistema e sua vizinhança. Essas trocas de
energia podem ser de dois tipos:
- Calor (q):
energia que entra ou sai do sistema em conseqüência da
diferença de temperatura entre sistema e vizinhança.
- Trabalho (w):
qualquer outra forma de energia diferente de calor, como
trabalho mecânico de expansão de um gás ou trabalho elétrico
fornecido por uma bateria.
OBS: Em laboratório de química, o trabalho mecânico
relacionado com expansão (ou compressão) de um gás é o mais
comum, pois um gás pode ser consumido ou produzido em uma
reação química, sob pressão externa constante, igual à
pressão atmosférica.
Exemplo:
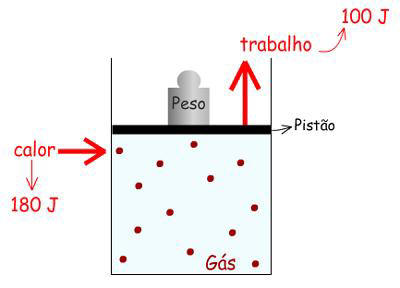 |
1) "q" vem da vizinhança que tem maior T
2) O gás absorve calor e eleva a sua T
3) O gás se expande e levanta o peso e o pistão,
ou seja, realiza "w"
|
Supondo-se que o sistema (gás) absorveu 180 J de calor
proveniente da vizinhança e, como conseqüência, realizou um
trabalho de expansão que forneceu à vizinhança 100 J de
trabalho.
Logo, o sistema ganhou energia sob forma de calor e perdeu
energia sob forma de trabalho.
Então:
|
∆E =
+180 J - 100 J = 80
J
|
| |
|
|
|
↓ |
|
| |
|
|
Variação líquida de Energia Interna |
Pode-se agora, enunciar o Primeiro Princípio da
Termodinâmica:
|
“Em qualquer processo a variação total de
Energia Interna do sistema (∆E), é
igual à soma do calor absorvido (q) e
do trabalho (w) realizado sobre o
sistema, ou seja, a Energia não é criada, nem
destruída, mas é conservada.”
|
Matematicamente: ∆E = q + w
As quantidades “q” e “w” têm módulo e
direção:
- Calor pode fluir para um sistema aumentando sua
temperatura ou deixar o sistema baixando sua temperatura.
- Um gás pode se expandir e realizar trabalho sobre a
vizinhança (empurrar a atmosfera) ou pode ser comprimido
quando a vizinhança empurra o gás e realiza trabalho sobre o
sistema.
Convenção moderna de sinais para “q” e “w”:
Calor (q):
- sinal (+): quando o sistema absorve energia sob forma de
calor,
- sinal (–): quando o sistema perde energia sob forma de
calor.
Trabalho (w):
- sinal (+): quando o sistema ganha energia sob forma de
trabalho – compressão,
- sinal (–): quando o sistema perde energia sob forma de
trabalho – expansão.
OBS: A convenção de sinal, para trabalho, apresentada acima,
é a recomendada atualmente pela IUPAC.
A convenção antiga (ainda encontrada em muitos livros) era:
Trabalho de expansão (+) e Trabalho de compressão (–).
Assim, na convenção antiga, o enunciado matemático do
Primeiro Princípio da Termodinâmica fica:
∆E = q – w |
| |
Como
medir o trabalho de expansão de um gás?
|
|
Na verdade, trabalho mecânico não se restringe a sistemas
gasosos, mas estes são mais facilmente imagináveis.
Considerando-se um sistema químico:
|
Zn0 (s) +
2 H+ (aq) →
Zn2+ (aq) +
H2 (g) q =
– 152,4 kJ / mol |
Quando esta reação ocorre em um béquer, sistema aberto, em
contato com a atmosfera, a reação é exotérmica e ocorre o
desprendimento de 152,4 kJ/mol de Zn consumido.
O Hidrogênio gasoso produzido aumenta o volume do sistema
(expansão), ou seja, o sistema realiza trabalho empurrando a
atmosfera.
Para calcular w,
pode-se imaginar que a atmosfera seja substituída por um
pistão sobre o qual atua a pressão atmosférica.
Supõe-se que o aumento de volume provocado pela produção de
H2 (g) seja
∆V:
Por definição:
|
w = – Fext x h |
| |
↓ |
| |
O sinal é negativo, pois a energia está saindo do
sistema como trabalho. |
Mas: Pext = Patm
= Fext / A onde: A =
área do pistão
Logo: Fext = Patm . A =
Pext x A
Substituindo: w =
– Pext x
A x h
Como: A x h =
∆V
Resulta: w =
– P∆V
Logo: o trabalho mecânico de expansão (ou compressão)
realizado (ou sofrido) contra uma pressão externa constante,
pode ser calculado por:
Retornando ao exemplo: 1 mol de Zn (s) produz
1 mol de H2 (g). A 25 ºC e 1 atm, 1 mol de H2
(g) ocupa o
volume de 24,45 L (calculado por PV = nRT).
O trabalho realizado pelo sistema químico ao empurrar a
atmosfera, ou seja ao exercer trabalho sobre a vizinhança
(atmosfera) é:
w = – 1
atm x (24, 45 L (Vf) –
0 L (Vi))
Lembrando que: 1 L.atm = 101,3 J
w = –
24, 45 atm.L x
101, 3 J / atm
. L
w = –
2476,78 J = – 2,48 kJ
Para se calcular ∆E:
∆E = q + w
∆E =
–152,4 kJ – 2,48 kJ
∆E =
– 154,88 kJ
Pode-se, no entanto, calcular o trabalho para um caso mais
geral, em que a pressão externa não é constante, dizendo que
uma variação infinitesimal de volume, dV, gera uma
quantidade infinitesimal de trabalho, dw. Então:
|
dw =
– Pext .
dV
e w total =
∑ dw
|
A pressão permanece virtualmente constante e igual a Pexterna
durante a variação infinitesimal de volume.
O trabalho efetuado durante o deslocamento finito é o
somatório (∑) dos trabalhos infinitesimais realizados
partindo do Estado inicial até a chegada no Estado final.
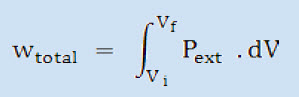
Esta relação geral permite calcular o trabalho desde que
seja conhecida a dependência da Pext
em função de V. |
| |
Trabalho e Calor são Funções de Estado?
|
|
O trabalho de expansão depende de como o sistema é conduzido
do Estado inicial para o Estado final. Pode-se imaginar dois
caminhos diferentes:
A figura mostra dois caminhos pelos quais o sistema pode
mudar do Estado Inicial (P1 V1)
para o Estado Final (P2 V2).
|
Em A:
|
1°) V1 → V2
o sistema é aquecido sob Pinterna constante
e igual a P1
2°) P1 → P2
o sistema é resfriado a V constante |
|
Em B: |
1°) P1 → P2
o sistema é resfriado a V constante
2°) V1 → V2
o sistema é aquecido sob Pinterna constante
e igual a P2. |
Como w =
– P ext .
∆V, os trabalhos realizados em cada caminho são
iguais às áreas marcadas. Logo: wA ≠ wB.
Conclusão: O trabalho realizado depende de como as
modificações são conduzidas, apesar dos Estados inicial e
final serem os mesmos. Logo, TRABALHO não é
Função deEstado, pois depende do caminho da
transformação.
Mas:
|
∆EA = ∆EB
pois E é
função de Estado |
|
∆EA = qA + w A ∆EB = qB + wB |
Como:
|
wA ≠ wB ,
então: qA ≠ qB
para ∆EA = ∆EB. |
Conclusão: O CALOR também não
é Função de Estado, pois depende do caminho da
transformação.
Para ocorrer uma mudança do Estado inicial (E1)
para o Estado final (E2) existem
diversos caminhos, conseqüentemente, diferentes combinações
possíveis de q + w para
um mesmo ∆E.
Exemplo:
Um sistema com volume de 25 L absorve 1000 J de calor.
Calcular ∆E para
o sistema quando:
a) q é
absorvido a V constante
V cte → w =
– P∆V =
O
∆E = q + w
∆E =
1000 J + 0 =
∆E =
1000 J ∆E = q
b) À
medida que “q” é absorvido, o sistema se expande
contra uma pressão externa constante de 1 atm até um volume
de 28,95 L.
w ≠ 0 → w =
– Pext . ∆V
w = – 1 atm (28,95 L – 25,0 L)
w = – 3, 95 atm. L x 101, 3 J / atm. L
w = – 400 J
∆E = q + w
∆E =
1000 J – 400 J
∆E =
600 J
c) À
medida que “q” é absorvido, o sistema se expande
contra uma pressão externa constante de 0,56 atm até um
volume de 42, 063 L.
w ≠ 0 → w =
– Pext . ∆V
w = – 0,
56 atm (42,63 L – 25,0 L)
w = – 9, 87 atm.L x 101, 3 J / atm. L
w = – 1000 J
∆E = q + w
∆E =
1000 J – 1000 J
∆E =
0 J Estado Inicial ≠ Estado Final, mas com o mesmo
valor de E |
Trabalho Reversível x Trabalho Irreversível
|
|
Supondo:
Estado Inicial: P =
10 atm e V =
1 L
Estado Final: P =
1 atm e V =
10 L
Qual o caminho que fornece a quantidade máxima de trabalho?
1) Expansão em 1 etapa:
|
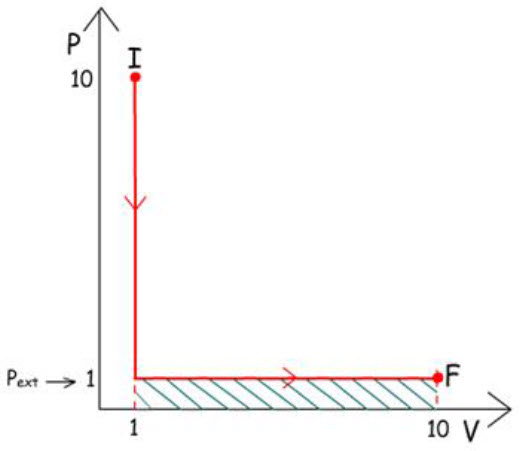 |
w =
– P∆V
w1 =
– 1 atm (10 – 1) L
w1 =
– 9 atm. L
|
|
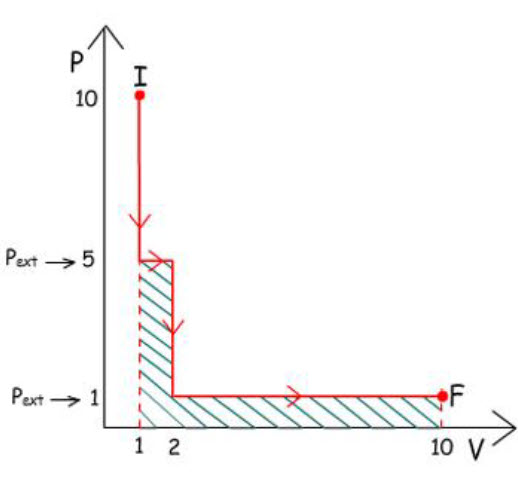
2) Expansão em 2 etapas:
|
|
w =
– P∆V
1ª Etapa: w =
– 5 atm (2 – 1) L w =
– 5 atm. L
2ª Etapa: w =
– 1 atm (10 – 2) L
w =
– 8 atm. L
w2 =
– 5 atm. L + (– 8 atm. L)
w2 =
– 13 atm. L
w2 > w1
|
|
Observa-se que se obtém mais trabalho quando a expansão é
realizada em duas etapas do que em uma única etapa.
O número de etapas pode ser aumentado:
3) Expansão em 3 etapas:
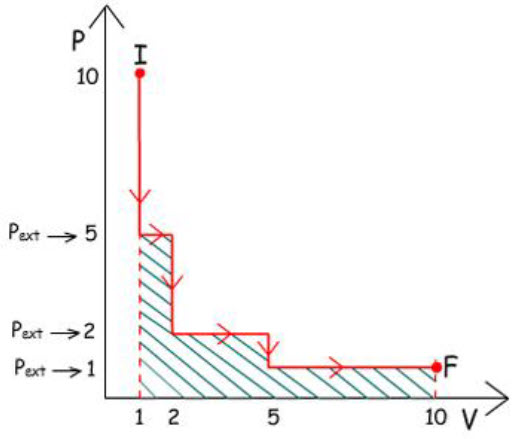 |
w =
– P∆V
1° Etapa: w =
– 5 atm (2 – 1) L
w =
– 5 atm. L
2° Etapa: w =
– 2 atm (5 – 2) L
w =
– 6 atm. L
3° Etapa: w =
– 1 atm (10 – 5) L
w =
– 5 atm. L
w3 =
– 5 atm. L + (– 6 atm. L) + (– 5 atm. L)
w3 =
– 16 atm. L
w3 > w2 > w1
|
|
Observa-se que se obtém mais trabalho ainda quando a
expansão é realizada em três etapas.
Pode-se deduzir que mais trabalho ainda pode ser obtido, se
a expansão for conduzida em mais etapas, nas quais a pressão
externa é mantida tão alta quanto possível.
Deve-se concluir que a maior quantidade de trabalho poderá
ser obtida se o processo for realizado em um número infinito
de etapas, sendo cada etapa uma expansão infinitesimal, nas
quais a Pext é
sempre ligeiramente menor do que a exercida pelo gás:
A expansão de um gás em infinitas etapas é um exemplo de
Processo Reversível.
Conclusão: O trabalho máximo que pode ser obtido de
uma transformação será obtido apenas se o processo for
conduzido de maneira reversível.
|
w máximo = w reversível
|
w reversível > w irreversível
|
Como um processo verdadeiramente reversível requer um número
infinito de etapas, levará um tempo infinito para ocorrer.
Portanto, nenhuma transformação real espontânea é reversível
e o trabalho que pode ser obtido em uma transformação
irreversível é sempre menor que o máximo teórico.
w irreversível < w máximo
(teórico)
|
Determinação de ∆E
|
|
Foi visto que: ∆E = q + w
Se a transformação é executada dentro de um recipiente
fechado, de forma que o volume do sistema se mantenha
constante, se tem:
∆V =
0 → não
ocorre variação de volume.
|
Conseqüência: |
w =
0 |
|
Resulta: |
∆E = q +
0 = q |
|
Logo: |
∆E = qV
, (qV =
calor trocado a volume constante). |
Conclusão: ∆E é
numericamente igual, ao calor absorvido (ou liberado) pelo
sistema, quando a transformação é realizada a volume
constante.
|
Entalpia
|
|
Entalpia (H) é uma função de Estado Termodinâmica
definida como:
H = E + P.V
|
Então: |
∆H = ∆E + ∆ (PV) |
(eq. 1) |
|
Relembrando que: |
∆E = q + w |
(eq. 2) |
|
E: |
w =
– P∆V |
(eq.3) |
Numa transformação à P constante:
Substituindo as equações 2, 3 e 4 na equação 1 se tem:
|
∆H = q – P∆V
+ P∆V
|
| |
↓ |
↓
|
| |
∆E
|
∆PV
à pressão constante
|
|
Resta: |
∆H = q |
|
|
Ou seja: |
∆H = q P |
(qP =
calor trocado a P constante) |
Em laboratório de química as reações são comumente
realizadas em recipientes abertos, ou seja, à pressão
constante (Pcte = Patm)
e não em condições de volume (V) constante.
Conseqüentemente o calor absorvido (ou perdido), nestas
condições não será qV (∆E),
e simqP (∆H).
Por esta razão, os químicos se interessam mais em medir ∆H do
que ∆E,
pois a entalpia (∆H) é uma Função
de Estado mais útil.
Assim:
∆H <
0 → o sistema perde calor a P constante → Processo
Exotérmico
∆H >
0 → o sistema absorve calor a P constante → Processo
Endotérmico
# Qual
a diferença entre ∆E e ∆H?
Sabe-se que: ∆H = ∆E +
∆(PV) (eq.
5)
Transformações que envolvem somente líquidos e/ ou sólidos:
∆(PV) = zero → ∆H = ∆E
Fases condensadas são muito pouco compressíveis, portanto ∆V é
muito pequeno (desprezível) e se P não
for muito elevada, podemos considerar ∆(PV) = 0.
# Transformações
que envolvem gases (produção ou consumo de gases),
geralmente:
..................................................................... ∆H ≠ ∆E.
Como PV = nRT → ∆(PV)
= ∆(nRT)
Para transformações a T constante:
∆(PV) = ∆(nRT)
= ∆n.RT
(eq. 6)
Onde: ∆n =
(n° de mols gasosos de produtos) – (n° de mols gasosos de
reagentes)
Substituindo eq.6, ∆(PV)
= ∆n. RT
na eq. 5:
∆H =
∆E + ∆n.
RT
|
Lembrete: |
R = 8, 314 J / mol. K |
| |
R = 1, 987 cal / mol. K |
Exemplos:
1) A
25 ºC e 1 atm, a reação de 1 mol de óxido de cálcio (CaO)
com água, libera 65,27 kJ, conforme a reação:
CaO(s) +
H2O (ℓ)→
Ca(OH)2 (s)
Quais são os valores molares de ∆H e ∆E para
este processo se as densidades de CaO(s), H2O(ℓ) e
Ca(OH)2(s) a
25 ºC são 3,25 g/mL, 0,997 g/mL e 2,24 g/mL,
respectivamente?
Resolução:
...................................................∆H =
qP ..........logo.......... ∆H =
- 65,27 kJ / mol
....................................como..........∆H = ∆E +
P∆V........ou ....∆E= ∆H -
P∆V
Cálculo de P∆V
..................................
...........................................................................Logo
................................................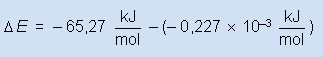
........................................................... ∆H
= -
65,27 kJ / mol
.................................Conclusão: .....∆H
» ∆E ..... (processos
envolvendo somente líquidos e sólidos)
2) A
25 ºC e 1 atm, a reação de produção de 1 mol de H2O (ℓ) a
partir de hidrogênio e oxigênio libera 285,57 kJ conforme a
reação:
H2(g) + ½ O2(g) → H2O(ℓ)
Quais são os valores molares de ∆H e ∆E para
este processo?
Resolução:
.........................................∆H =
qP ..........logo........∆H. =
- 285,57 kJ / mol
.................................................................Lembrando
que: PV = nRT
Logo
P∆V = ∆n.R.T
sabendo que ∆E= ∆H -
P∆V
ou seja
∆E= ∆H - ∆n.R.T
Como ∆n
= 0 - 1,5 = -1,5.... e.... R
= 8,314 J / mol.K
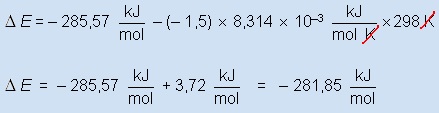
Logo
∆E
» -281,85
kJ / mol
Conclusão: ........∆H
≠ ∆E ..... (existem
gases envolvidos no processo)
|
Calorimetria
|
|
Um dos procedimentos usados para medir o calor gerado por
uma reação exotérmica é através de uma técnica chamada Calorimetria.
Antes de se estudar esta técnica, é preciso definir algumas
propriedades térmicas, que descrevem a capacidade de um
sistema absorver ou liberar calor sem que ocorra
transformação química. Estas propriedades são:
- Calor específico (c)
- Capacidade calorífica (C)
- Capacidade calorífica molar (Cm)
Calor Específico (c)
Calor específico de uma substância é a quantidade de calor
necessária para aumentar a temperatura de um (1) grama da
substância em 1 °C (ou 1 K).
Unidades utilizadas: J / g. K
(SI), J / g. ºC,
cal / g. K
ou cal / g. ºC
(sendo as duas últimas encontradas em livros antigos).
Exemplos:
cágua =
1 cal / g.ºC = 4,184 J / g. ºC
cFerro =
0,4498 cal / g .ºC
ccobre =
0,387 cal / g .ºC
Para 1 g: c = q / ∆T
logo: q = c. ∆T
Para uma massa “m” qualquer:
q = m. c.
∆T
Exemplo:
Qual a quantidade de energia absorvida por um anel de ouro,
com massa igual a 5,5 g, se sua temperatura aumentar de 25
ºC para 28 ºC?
Dado: cAu =
0,129 J / g .ºC
Resolução:
mAu =
5,5 g
cAu =
0,129 J / g .ºC
Ti =
25 °C
Tf =
28 °C
∆T =
(28 – 25) ºC = 3 ºC
∆T >
0 significa que o anel aqueceu, absorveu calor
q = m. c. ∆T
q absorvido =
5,5 g x
0,129 J / g. ºC x
3 ºC
q abs =
2,1 J
Capacidade Calorífica (C)
Capacidade calorífica de um objeto é a quantidade de calor
associada com a variação da temperatura do objeto em 1 ºC ou
1 K.
A capacidade calorífica depende do material de que é feito o
objeto e da sua massa.
Unidades: J / K (SI), J / ºC, cal / K ou cal / ºC (sendo as
duas últimas encontradas em livros antigos).
OBS: A capacidade calorífica de um objeto informa
tanto a quantidade de calor que ele absorve para elevar a
sua temperatura quanto à quantidade de calor que este deve
perder para que ocorra um dado decréscimo de temperatura.
Como este conceito se aplica a qualquer objeto, pode ser
empregado a um calorímetro de bomba,
incluindo todos os objetos imersos na água e também as
paredes do recipiente que contém a água.
Uma melhor definição:
|
“capacidade calorífica é
a quantidade de calor necessária para aumentar 1
ºC (ou 1 K) a temperatura do objeto, ou a
quantidade de calor que o objeto deve perder
para sua temperatura diminuir 1 ºC (ou 1 K).”
|
|
Se tem: |
C = q / ∆T |
|
| |
q = C.
∆T |
|
|
Se: |
∆T <
0 |
(Tf < Ti)
→ objeto perde calor e q < 0 |
|
Se: |
∆T >
0 |
(Tf > Ti)
→ objeto ganha calor e q > 0 |
|
| |
Capacidade
Calorífica Molar
|
|
Capacidade Calorífica Molar (Cm)
de uma substância, é a quantidade de calor necessária para
elevar de 1 ºC (ou 1K) a temperatura de 1 mol desta
substância.
Unidades: J / mol. K
(SI), J / mol. ºC,
cal / mol. K
ou cal / mol. ºC
(sendo as duas últimas encontradas em livros antigos).
Exemplo: Cm (H2O)
= 75,2 J / mol. ºC
|
Para 1 mol: |
Cm = q / ∆T |
|
Logo: |
q = Cm . ∆T |
|
Para “n” mols: |
q = n . Cm .
∆T |
Exemplo:
Supondo que 15,0 g de cobre são aquecidos de 16,1 ºC a 49,3
ºC sob pressão atmosférica. Calcular o calor absorvido neste
processo admitindo que a capacidade calorífica do cobre não
varia neste intervalo de temperatura.
Dado:Cm (Cu)
= 24,59 J / mol .ºC
Resolução:
mCu =
15,0 g
Cm (Cu) =
24,59 J / mol .ºC
Ti =
16,1 ºC
Tf =
49,3 ºC
∆T = (49,3 – 16,1) ºC = 33,2 ºC → ∆T
> 0 Cobre foi aquecido, absorveu calor
Cálculo do valor de n: nCu = m / M
nCu =
15,0 g / 63,54 g. mol-1 = 0,236 mol
Cálculo da quantidade de calor absorvido pelo cobre:
q = n . Cm. ∆T
q absorvido =
0,236 mol x 24,59 J / mol .ºC
x 33,2 ºC
q abs =
192,67 J |
| |
Capacidade Calorífica Molar de Gases
|
|
A Capacidade Calorífica Molar mede a quantidade de calor
necessária para aquecer 1 mol de uma substância em 1 ºC (ou
1 K).
No entanto, se esta substância for um gás, a capacidade
calorífica molar depende
das condições de aquecimento, pois o calor não é
Função de Estado. À pressão constante, parte do calor
absorvido é usada para realizar trabalho de expansão e não
para o aquecimento do gás.
Definições:
CV,m = qV /
∆T = ∆E /
∆T
onde, CV,m =
Capacidade Calorífica Molar a volume constante e qV =
calor absorvido pelo sistema, quando a transformação é
realizada a volume constante.
CP,m = qP /
∆T = ∆H /
∆T
onde, CP,m =
Capacidade Calorífica Molar a pressão constante e qp =
calor absorvido pelo sistema, quando a transformação é
realizada a pressão constante.
OBS: As capacidades caloríficas molares a volume e pressão
constantes de sólidos e líquidos têm valores comparáveis e,
portanto, não se faz distinção.
Sólidos e líquidos CP,m  CV,m CV,m |
| |
Qual a diferença entre CP,m e CV,m de
gases?
|
|
Tem: |
H = E + PV |
|
para um (1) mol: |
PV = RT |
|
logo: |
H = E +
RT |
|
e: |
∆Hm = ∆Em +
R. ∆T
(÷∆T) |
| |
∆Hm / ∆T = ∆Em / ∆T
+ RT / ∆T |
| |
CP,m = CV,m
+ R |
Exemplo:
Calcular a capacidade calorífica molar (CP,m)
do Argônio (Ar).
Dado: CV,m.=
12,8 J/mol .ºC
Utilizando as equações acima se obtém:
CP,m =
12,8 J / mol .ºC
+ 8, 314 J / mol .ºC
CP,m =
21, 114 J / mol .ºC |
| |
Calorímetro
|
|
Muitos calores de reação são determinados medindo-se a
variação de temperatura causada pelas trocas de calor entre
a mistura da reação (sistema) e o conteúdo de um calorímetro (vizinhança),
onde a mistura é colocada.
Existem vários tipos de calorímetros, serão comentados: o
calorímetro de bomba e o calorímetro de solução.
Calorímetro de Bomba ou Bomba Calorimétrica
É um calorímetro sofisticado que mede o calor trocado em
condições de volume constante.
Mede qV = ∆E.
No calorímetro de bomba, a amostra é colocada no vaso
interno, chamado bomba, e a combustão se inicia por ignição
elétrica. Uma vez iniciada a combustão, a energia liberada
como calor se difunde pelas paredes da bomba até a água. O
calor liberado pela reação é proporcional à variação de
temperatura de todo o conjunto do calorímetro. Como o volume
da câmara é fixo, não há variação de volume, logo ∆V é
zero e o calor liberado pela reação, a volume constante, é
igual ao calor absorvido pela bomba.
P∆V =
zero,
– qV (liberado pela
reação) = qbomba (absorvido pela
bomba)
qabs. bomba = Cbomba x ∆T
Calorímetro de Solução
É um calorímetro simples, muitas vezes improvisado e que
mede o calor trocado em condições de pressão constante.
Mede qP = ∆H.
Dois copos de plástico são encaixados e cobertos por uma
tampa. A reação exotérmica ocorre na solução aquosa contida
no copo interno. O isolamento térmico proporcionado pelos
copos é suficiente para manter o calor confinado na solução.
A variação de temperatura da solução contida no copo pode
ser medida com um termômetro.
– qP (liberado
pela reação) = q (absorvido
pela solução)
e
qabs. solução = msolução x csolução x ∆T
Se a solução é diluída, pode-se considerar csolução » cágua,
sem erro apreciável.
Exemplos:
1) Calcule
o ∆H de
combustão de 1 mol de Tolueno a 1 atm e 25 ºC, sabendo que
0,05 mol de Tolueno (C7H8(ℓ))
é queimado em uma bomba calorimétrica provocando um aumento
de temperatura de 3,075 ºC. A capacidade calorífica desta
bomba é 64,12 kJ / ºC.
Resolução:
Primeiramente deve-se escrever a reação química devidamente
balanceada.
C7H8(ℓ)
+ 9 O2(g) → 7 CO2(g) + 4
H2O(ℓ)
Em uma bomba calorimétrica:
qabs. bomba = Cbomba x ∆T
desta forma:
q abs
bomba =
64,12 kJ / ºC x 3,075 ºC
q abs
bomba = 197,17 kJ
Como:
qbomba (absorvido
pela bomba) = – qV (liberado
pela reação)
O calor a volume constante liberado
pela reação é igual ao calor
absorvido pela bomba calorimétrica.
Lembra-se, então que a quantidade de calor é igual porém o
sentido do fluxo de energia é oposto, o que justifica a
troca de sinal acima.
|
Para 0,05 mol se tem: |
q liberado
reação =
– 197,17 kJ (qV = ∆E) |
|
Para 1 mol: |
qV = ∆Em =
– 197,17 kJ / 0,05 mol |
| |
∆Em =
– 3943,4 kJ . mol-1 |
|
Mas: |
∆Hm = ∆Em
+ ∆n RT |
calculando ∆n gasosos: ∆n(g)
= n (CO2) – n (O2) =
7 – 9 = – 2
∆Hm =
– 3943,4 kJ. mol-1 +
(–2) . 8,
314 x 10-3 kJ. mol-1 . K-1 x
298 K
∆Hm =
– 3948,36 kJ. mol-1
2) Quando
250 mL de HCl 1 mol/L a 25 ºC foram misturados com 350 mL de
NaOH 0,8 mol/L também a 25 ºC, num calorímetro de solução, a
temperatura da mistura reagente aumentou para 29,86 ºC.
Calcular ∆H molar
de neutralização.
Dados: cágua
= 4,184 J / g. ºC
Resolução:
Primeiramente devemos escrever a reação química devidamente
balanceada.
|
HCl(aq) +
|
NaOH(aq) ®
|
NaCl(aq) +
|
H2O(ℓ)
|
|
250 mL
|
350 mL
|
650 mL
|
|
1 mol / L
|
0,8 mol / L
|
|
|
|
25 ºC
|
29,86 ºC
|
Cálculo do número de mols de ácido e de base, lembrando
que: n =
conc x volume,
Ou seja, mol / L x L =
mol
nHCl = 1 mol/L x 0,250 L = 0,25 mol → Reagente
limitante
nNaOH = 0,8 mol/L x 0,350 L = 0,28
mol
csolução » cágua
= 4,184 J / g. ºC
msolução » 600
g (ρsolução » ρágua=
1 g/mL)
∆T = 29,86 ºC – 25 ºC = 4,86
ºC
Em uma solução:
qabs pela
solução = msolução x csolução x ∆T
desta forma:
qabs pela
solução = 600 g x 4,184 J / g. ºC
x 4,86 ºC
qabs pela
solução = 12.200,54 J
Como:
qabs solução
= – qP (liberado
pela reação)
e qp = ∆H
(reação a pressão constante)
qlib pela reação = – 12.200,54 J
O calor a pressão constante liberado
pela reação é igual ao calor
absorvido pela solução. Lembra-se, então que a
quantidade de calor é igual porém o sentido do fluxo de
energia é oposto, o que justifica a troca de sinal acima.
|
Para 0,25 mol temos: |
q liberado
reação =
– 12.200,54 J (qP = ∆H) |
|
Para 1 mol: |
qP = ∆Hm =
– 12.200,54 J / 0,25 mol |
| |
∆Hm =
– 48.802,16 J / mol |
| |
∆Hm =
– 48,80 kJ / mol |
|
Termoquímica
|
|
É possível determinar a variação de entalpia (∆H)
em qualquer transformação física ou química.
Numa reação química, os produtos constituem o sistema no
estado final e os reagentes o sistema no estado inicial.
Então:
|
∆H reação
= H produtos
– H reagentes
|
Como foi visto anteriormente, ∆H associado
a qualquer processo pode ser calculado, diretamente, pelo
calor liberado (ou absorvido) pelo sistema a pressão
constante, qp,
ou indiretamente a partir da medida do calor absorvido (ou
liberado) a volume constante, qv,
e então aplicar:
A grandeza geralmente usada para reações químicas é a Variação
de Entalpia Padrão Molar a 25 ºC (∆H°m,
298), que pode ser definida como:
∆H°m, 298 é
a variação de entalpia do sistema por mol de reação, quando
os reagentes são transformados em produtos, ambos no seu Estado
Padrão a 298
K.
O Estado
Padrão de uma
substância é a sua forma mais estável a 1 bar de pressão.
OBSERVAÇÕES:
1) Lembrando
que:
| 1 atm = |
1,01325 x 105 Pa e que |
| |
1 bar = 105 Pa, |
| Logo: |
1 atm » 1
bar |
2) Os
dados termodinâmicos são, na maioria das vezes, registrados
a 298,15 K (25 ºC). A temperatura não faz parte da definição
de Estado Padrão. Pode-se ter um Estado Padrão em qualquer
temperatura, mas 298,15 K é a temperatura mais comum usada
nas coletas de dados.
3) Parte
da literatura define a pressão do Estado Padrão como sendo 1
bar (recomendado pela IUPAC), e não 1 atm.
Exemplo:
|
C(grafita) + O2(g)
→ CO2(g)
|
∆H°m,
298 =
– 393,51 kJ. mol -1 |
|
↓
Equação Química
|
|
|
↓
Equação Termoquímica
|
A equação termoquímica é a equação química acompanhada da
variação de energia,∆H°m, 298,
que é denominada Entalpia
Padrão Molar de Formação do CO2 na
temperatura de 298,15 K.
Significa que, 1 mol de CO2 é
formado a partir seus elementos na sua forma mais estável,
isto é 1 mol de C(grafita) e
1 mol de gás oxigênio, estando todos (reagentes e produtos)
a 1 bar e 298,15 K. E ainda que foram liberados 393,51 kJ de
calor.
A combustão de C(grafita) pode
ser efetuada quantitativamente em um calorímetro de bomba,
permitindo a determinação de ∆H,
basta colocar 1 mol de C(grafita) em
excesso de O2para obter-se a combustão completa.
Este processo também é válido para a reação:
|
CO(g) + ½ O2(g)
→ CO2(g) ∆H°m,
298 =
– 282,98 kJ. mol -1
|
É necessário também colocar 1 mol de CO em presença de
excesso de O2 para
que ocorra a conversão completa a 1 mol de CO2.
Por outro lado, a combustão parcial do C(grafita) a
CO, é difícil de ser efetuada quantitativamente.
|
C (grafita)
+ ½ O2(g) → CO(g) ∆H°m,
298 =
?
|
Sem excesso de oxigênio a combustão do C(grafita) é
incompleta, mas com excesso de O2o CO pode ser
oxidado a CO2.
Mas: como a Entalpia é Função
de Estado, torna-se desnecessária a determinação direta.
Pode-se chegar ao valor acima desejado, imaginando-se que
existem duas maneiras de se combinar C grafita e O2 para
se obter CO2.
A figura abaixo mostra os dois caminhos:
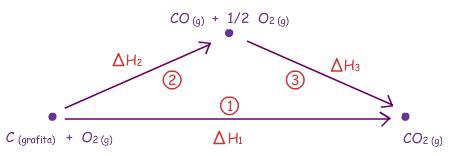
 a
reação pode ocorrer diretamente através do caminho 1 para
o qual ∆H1é
conhecido. a
reação pode ocorrer diretamente através do caminho 1 para
o qual ∆H1é
conhecido.
 a
reação pode ocorrer em duas etapas: 2 e 3,
das quais somente se conhece ∆H3. a
reação pode ocorrer em duas etapas: 2 e 3,
das quais somente se conhece ∆H3. |
Mas como Entalpia
é Função de Estado, ∆H para
a transformação de C(grafita) em
CO2 é independente
do caminho, o que significa que:
∆H1 = ∆H2 + ∆H3
Como ∆H1 e ∆H3 podem
ser medidos experimentalmente:
∆H1 =
– 393, 51 kJ. mol -1
∆H3 =
– 282,98 kJ. mol -1
Então:
∆H2 = ∆H1 – ∆H3
∆H2 =(
– 393,51 kJ. mol -1)
– (– 282,98 kJ. mol –1)
∆H2 = – 110,53 kJ. mol –1
E:
H2 representa
a variação de entalpia padrão para a transformação do C(grafita) em
CO(g), desta forma a equação termoquímica fica
representada da seguinte forma:
|
C(grafita) + ½ O2(g)
® CO(g) ∆H°m,
298 =
– 110,53 KJ. mol –1
|
|
Lei de Hess
|
|
O calor liberado ou absorvido em uma reação química, à
pressão constante, é independente do caminho seguido pela
reação.
A figura anterior equivale à combinação algébrica de reações
químicas cujos ∆H são
conhecidos, de modo a se obter a reação desejada e para
calcular a variação de entalpia desta reação, é preciso
combinar algebricamente os valores conhecidos de ∆H de
forma análoga ao procedimento utilizado com as reações
químicas.
|
Assim:
C(grafita) + O2(g)
→ CO2(g) |
x (1) |
|
CO(g) + ½ O2(g)
→ CO2(g)
|
x (– 1)
|
|
Resulta: |
|
| |
½ O2(g) |
|
|
| C(grafita) + |
O2(g) |
® |
CO2(g) |
|
∆H°m,298=–393,51 kJ. mol-1
|
|
+ CO2(g)
→ CO(g) + ½
O2(g)
|
∆H°m,298=+282,98 kJ. mol-1
|

|
|
C(grafita) + ½ O2(g)
→ CO(g)
|
∆H°m, 298 = – 110,53
kJ. mol -1
|
Outro exemplo:
Deseja-se obter o valor de ∆H°m,
298 na seguinte equação química:
| C(grafita) + 2 H2(g)
→ CH4(g) ∆H°m,
298 =
? |
É possível determinar experimentalmente os seguintes valores
de ∆H°m,
298 e por
observação determinar o fator adequado para multiplicar cada
reação:
Assim:
|
Assim:
C(grafita) + O2(g) →
CO2(g) |
∆H°m,298=–
393,51 kJ. mol -1
x (1) |
|
H2(g) + ½ O2(g)
→ H2O(ℓ)
|
∆H°m,298=–
285,83 kJ. mol -1
x (2)
|
|
CH4(g) + 2 O2(g) → CO2(g)
+ 2 H2O(ℓ)
|
∆H°m,298=–
890,36 kJ. mol -1
x (–1)
|
|
Resulta: |
|
|
C(grafita) + O2(g)
→ CO2(g)
|
∆H°m, 298 =
– 393,51 kJ. mol -1
|
|
2 H2(g) + O2(g)
→ 2
H2O(ℓ)
|
∆H°m, 298 =
– 571,66 kJ. mol -1
|
|
CO2(g) + 2
H2O(ℓ)
→ CH4(g) + 2
O2(g)
|
∆H°m, 298 =
+ 890,36 kJ. mol -1
|

|
|
C(grafita) + 2 H2(g)
→ CH4(g)
|
∆H°m, 298 =
– 74,81 kJ. mol –1
|
O uso da Lei de Hess, permite evitar um grande número de
experimentos calorimétricos de difícil execução.
Pode-se armazenar, de forma eficiente, informações
termoquímicas conhecidas, (ou por que foram determinadas
experimentalmente ou por que foram calculadas através da Lei
de Hess), por meio da compilação de tabelas de Entalpia
Molar de Formação a 298,15 K e Entalpia
Padrão Molar de Combustão a 298,15 K.
|
Entalpia Padrão Molar
|
|
— de Formação a 298,15 K: É
a variação de entalpia da reação
de formação de
1 mol do composto puro no Estado Padrão, a partir de seus
elementos também no Estado Padrão, na temperatura de 298,15
K. Exemplos:
|
C(grafita) + O2(g)
® CO2(g) |
∆Hf°298 =
– 393,51 kJ . mol-1 |
|
C(grafita) + ½ O2(g)
® CO(g)
|
∆Hf°298 =
– 110,53 kJ . mol-1
|
|
C(grafita) + 2 H2(g)
® CH4(g)
|
∆Hf°298 =
– 285,83 kJ . mol-1
|
|
2 H2(g) + ½ O2(g)
® H2O(ℓ)
|
∆Hf°298 =
– 74,81 kJ . mol-1
|
OBS: Por definição, ∆Hf°298 de
todas as substâncias simples no seu estado padrão é igual a zero.
Para substâncias compostas os valores de ∆Hf°298 são
encontrados nas tabelas
com os resultados termodinâmicos, nos livros
indicados na bibliografia.
— de Combustão a 298,15 K: É
a variação de entalpia da reação
de combustão de
1 mol do composto puro no Estado Padrão, formando CO2(g) e
H2O(ℓ) também
no estado padrão, a 298,15 K.
Exemplo:
|
CH4(g) + 2 O2(g)
® CO2(g)
+ 2 H2O(ℓ) ∆HC°m,
298 =
– 74,81 kJ . mol-1
|
|
Utilização
das Tabelas Termodinâmicas
|
|
Como deve-se utilizar as tabelas com os resultados
termodinâmicos para calcular o valor da entalpia padrão de
reação, ∆Hr°298?
A tabela de entalpia padrão de formação, ∆Hf°m,
298, permite calcular o valor da entalpia (∆Hr°298 )
de qualquer reação química a 25 ºC, como no exemplo a
seguir.
Exemplo:
Deseja-se calcular o ∆H da
reação abaixo, a 298,15 K.
|
HCOOH(ℓ)
→ CO(g) + H2O(ℓ) ∆Hr°,
298 =
?
|
Consultando a tabela, obtém-se os valores de ∆Hr°,
298 para
HCOOH(ℓ),
CO(g) e
H2O(ℓ).
Deve-se escrever as reações de formação de cada substância,
com o respectivo valor de ∆Hf°,
298 .
| C(grafita) + ½ O2(g)
® CO(g) |
∆Hf°,
298 =
– 110,53 kJ. mol-1
(eq. 1) |
| H2(g) + ½ O2(g) ®
H2O(ℓ) |
∆Hf°,
298 =
– 285,83 kJ. mol-1
(eq. 2) |
| H2(g) + O2(g) + C(grafita)
® HCOOH(ℓ) |
∆Hf°,
298 =
– 424,72 kJ. mol-1
(eq. 3) |
Imaginando
que esta reação pode ser conduzida por um caminho
alternativo, utilizam-se as informações termoquímicas da
seguinte forma:
1°) O
Ácido Fórmico se decompõe em C(grafita), H2(g) e
O2(g).
2°) Estes
elementos reagem formando CO(g) e
H2O(ℓ).
| |
C(grafita) + H2(g) + O2(g) |
|
|
∆H2 |
|
∆H3 |
| |
∆H1 |
|
|
HCOOH(ℓ) |
|
CO(g) + H2O(ℓ) |
Pela Lei de Hess:
Mas:
|
∆H3 = ∆Hf°m,
298 (CO(g))
+ ∆Hf°m,
298 (H2O(ℓ))
|
(eq. 5)
|
|
∆H2 =
– ∆Hf°m,
298 (HCOOH(ℓ))
|
(eq. 6)
|
 Como a reação 2 representa o caminho de decomposição
do ácido fórmico, o seu valor de ∆H2 é
igual àrecíproca do
valor de ∆Hf°m,
298 ,
reação oposta a da formação do Ácido Fórmico a partir de
seus elementos.
Como a reação 2 representa o caminho de decomposição
do ácido fórmico, o seu valor de ∆H2 é
igual àrecíproca do
valor de ∆Hf°m,
298 ,
reação oposta a da formação do Ácido Fórmico a partir de
seus elementos.
– ∆Hf°m,
298(HCOOH(ℓ))
= ∆H°dec,
m, 298 (HCOOH(ℓ))
Substituindo as (eq. 5) e (eq. 6) na (eq. 4) tem-se:
|
∆H1 =
|
∆Hf°m, 298 (CO(g))
+ ∆Hf°m,
298, 298 (H2O(ℓ)) |
–
|
∆Hf°m,
298, 298 (HCOOH(ℓ))
|
| |
↓
|
|
↓
|
| |
∆H3
|
+
|
∆H2
|
Calculando:
|
∆H1 =
– 110,53 kJ. mol-1
– 285,83 kJ. mol-1
+ 424,72 kJ. mol-1
|
|
∆H1 =
28,36 kJ. mol-1
|
Pode-se observar a partir deste exemplo, que o ∆Hr°298 de
qualquer reação química pode ser calculado a partir dos
valores de ∆Hf°m,
298 de
reagentes e produtos:
∆Hr°m, 298 = Σ∆Hf°m,
298 (Produtos)
– Σ∆Hf°m,
298 (Reagentes)
Pois qualquer reação pode, teoricamente, ser conduzida por
um caminho em que:
1°) Reagentes
se decompõe em seus elementos:
( – ∆Hf°m,
298 dos
reagentes)
2°) Produtos
são formados a partir dos seus elementos:
( + ∆Hf°m,
298 dos
produtos)
OBS: Algumas substâncias simples, por não estarem no Estado
Padrão, possuem ∆Hf°m,
298 diferente
de zero.
Exemplos:
|
Br2 (g)
|
∆Hf°m, 298 =
+ 30,91 kJ. mol-1
calor de vaporização do Br2 |
Estado padrão: Br2(ℓ) |
|
I2 (g) |
∆Hf°m, 298=
+ 62,44 kJ. mol-1
calor de sublimação do I2 |
Estado padrão: I2(s) |
|
C(s), diamante |
∆Hf°m, 298 =
+ 1,895 kJ. mol-1 |
Estado padrão: C(s), grafita |
|
S(s), monocíclico |
∆Hf°m, 298 =
+ 0,33 kJ. mol-1 |
Estado padrão: S(s), rômbico |
|
P4(g) |
∆Hf°m, 298 =
+ 58,91 kJ. mol-1 |
Estado Padrão: P(s), branco |
|
Aplicando os
conhecimentos
|
|
Calcular a entalpia padrão da reação de glicose com
oxigênio.
|
C6H12O6(s)
+ 6 O2(g) → 6 CO2(g)
+ 6 H2O(ℓ)
|
1) Lembrando
o que é a reação de combustão:
A reação de um mol compostos orgânicos com oxigênio, gerando
CO2 e
H2O é chamada uma reação de combustão, logo o ∆Hr°298 é
a entalpia padrão de combustão da glicose,∆Hc°298 (glicose).
2) Obtendo
os valores das entalpias padrão de formação, ∆Hf°298,
dos reagentes e produtos, através da consulta à tabela de
resultados termodinâmicos.
|
∆Hf°298 C6H12O6(s) =
– 1268 kJ. mol-1
|
|
∆Hf°298 CO2(g)
= – 393,51 kJ. mol-1
|
|
∆Hf°298 H2O(ℓ)
= – 285,83 kJ. mol-1
|
|
∆Hf°298 O2(g)
= ZERO
|
3) Escrevendo
as relações entre os ∆H.
|
∆Hr°298 = Σ∆Hf°m,
298 (Produtos)
– Σ∆Hf°m,
298 (Reagentes)
|
e lembrando que: ∆Hr°298 = ∆Hc°m,
298
|
∆Hr°298=[6
x ∆Hf°m,
298 (CO2(g))
+ 6 x ∆Hf°m,
298 (H2O(ℓ))]
– [∆Hf°m,
298 (C6H12O6(s))
+ 6 x ∆Hf°m,
298 O2(g)] |
4) Substituindo
os valores:
|
∆Hr°298=[6x(–393,51kJ.mol-1)+6x(–285,83
kJ.mol-1)] – [–1268kJ.mol-1+6x0] |
|
∆Hr°298
= [ (– 2361,06 kJ. mol-1)
+ (– 1714,98 kJ. mol-1)]
– (– 1268 kJ. mol-1) |
|
∆Hr°298 =
– 4076,04 kJ. mol-1
+ 1268 kJ. mol-1 |
|
∆Hr°298
= ∆Hc°m,
298 (C6H12O6(s))
= –2808,04 kJ. mol-1 |
|
Entalpia de
Mudança de Fase
|
|
Mudanças de fase em que as moléculas ficam mais separadas
requerem energia e, portanto são endotérmicas.
Mudanças de fase que aumentam o contato entre as moléculas
liberam energia e, portanto são exotérmicas.
Como as mudanças de fase ocorrem tipicamente à pressão
constante, podemos identificar a transferência de calor que
acompanha a mudança de fase com uma alteração da entalpia da
substância.
Exemplos:
|
∆Hvaporização = H vapor – H líquido
|
|
∆H vaporização >
O
|
∆H condensação <
O
|
|
∆H fusão >
O
|
∆H solidificação <
O
|
|
∆H sublimação >
O
|
|
|
∆H vaporização =
– ∆H condensação
|
|
∆H fusão =
– ∆H solidificação
|
Relembrando as mudanças de estado físico (clique aqui)
Como Entalpia é uma Função de Estado, a entalpia de
sublimação de uma substância é a mesma, se a transição
ocorre em:
uma etapa:
S → G, ou
em duas etapas:
1ª) S →
L
2ª) L →
G.
onde: S =
sólido, G =
gás e L =
líquido.
A Entalpia de sublimação de uma substância deve ser igual à
soma das entalpias de fusão e vaporização medidas na mesma
temperatura.
∆H sublimação
= ∆H fusão
+ ∆H vaporização
|
Entalpia de Ligação
|
|
Em uma reação química, as ligações existentes são quebradas
e novas ligações são formadas. Pode-se estimar a entalpia de
reação, se forem conhecidas as variações de entalpia que
acompanham a quebra e a formação de ligação.
A energia de uma ligação química é medida pela entalpia
de ligação (∆HL°),
que é a diferença entre as entalpias padrão molar (H°m)
da molécula XY (X
– Y) e de seus fragmentosX e Y.
∆HL°m =
[H°m (X(g))
+ H°m (Y(g))
] – [H°m (XY(g))]
Enquanto a entalpia
de rede é
igual ao calor necessário (em pressão constante) para
quebrar um (1) mol de substância iônica, a entalpia
de ligação é
igual ao calor necessário para quebrar um (1) mol de
ligações à pressão constante.
Exemplo:
|
H2 (g) → 2 H (g)
|
∆HL°m =
+ 436 kJ
|
|
|
↓
|
|
|
Entalpia de ligação do H2
|
|
|
|
|
2 H (g)
® H2 (g) ∆H°m =
– 436 kJ
|
Pode-se escrever ∆HL°m (H
– H) = + 436 kJ. mol-1, o que significa:
# 436
kJ são necessários para dissociar um (1) mol de H2 em
átomos.
# 436
kJ são liberados quando átomos de H se combinam para formar
um (1) mol de H2.
Em resumo: a quebra de
uma ligação é sempre endotérmica,
enquanto a formação de
uma ligação é sempre exotérmica.
A tabela abaixo lista as entalpias de ligação de algumas
moléculas diatômicas:
|
Molécula |
∆HL°m
(kJ.mol-1) |
Molécula |
∆HL°m
(kJ.mol-1) |
|
H2 |
436 |
Br2 |
193 |
|
N2 |
944 |
I2 |
151 |
|
O2 |
496 |
HF |
565 |
|
CO |
1074 |
SCl |
431 |
|
F2 |
158 |
HB+ |
366 |
|
Cl2 |
242 |
HI |
299 |
|
ATKINS, P., JONES, L., Princípios
de química: questionando a vida moderna e o meio
ambiente. 3. ed. Porto Alegre: Bookman,
2006. p.336. |
Em moléculas poliatômicas, todos os átomos atraem todos os
elétrons da molécula, como resultado, a energia de ligação
entre um determinado par de átomos varia pouco de um
composto para outro.
Exemplo:
a) entalpia de ligação O – H
em HO – H
é 492 kJ.mol-1.
b) entalpia de ligação O – H
em CH3O – H
é 437 kJ.mol-1.
Essas variações de entalpia de ligação não são consideradas
muito grandes, de forma que as entalpias
de ligação médias, representadas por ∆HL°m,
são tabeladas e servem como guia para avaliar a energia de
ligação em qualquer molécula.
Os valores tabelados são para amostras na fase gasosa. A
tabela abaixo exemplifica algumas entalpias de ligação
médias.
|
Ligação |
∆HL°m (kJ.mol-1) |
Ligação |
∆HL°m (kJ.mol-1) |
| C–H |
412 |
C–I |
238 |
| C–C |
348 |
N–H |
388 |
| C=C |
612 |
N–N |
163 |
| C,C
no Benzeno |
518 |
N=N |
409 |
| C≡C |
837 |
N–O |
210 |
| C–O |
360 |
N=O |
630 |
| C=O |
743 |
N–F |
195 |
| C–N |
305 |
N–Cl |
381 |
| C–F |
484 |
O–H |
463 |
| C–Cl |
338 |
O–O |
157 |
| C–Br |
276 |
|
|
|
ATKINS, P., JONES, L., Princípios
de química: questionando a vida moderna e o meio
ambiente. 3. ed. Porto Alegre: Bookman,
2006. p.337. |
As entalpias de reação podem ser estimadas usando-se as
entalpias de ligação médias para determinar a energia total
necessária para quebrar ligações dos reagentes e a energia
total liberada para formar as ligações dos produtos.
Determinar entalpia de reação através das entalpias de
ligação equivale a imaginar que todos os reagentes se
separam em seus átomos e que estes átomos se recombinam para
formar produtos. Na prática, só as ligações que sofrem
alterações são consideradas.
Como as entalpias de ligação referem-se às substâncias na
fase gasosa, todas as espécies devem ser gases ou
convertidas à fase gasosa.
Exemplo: Para estimar-se a entalpia padrão da reação:
Ligações rompidas
2 ligações C–Cl: 2 × 338 kJ.mol-1 = 676 kJ
2 ligações H–F: 2 × 565 kJ.mol-1 = 1130
kJ
+ 1800
kJ →→→ Energia
absorvida
Ligações formadas
2 ligações C–F: 2 ´ (- 484 kJ.mol-1) = – 968 kJ
2 ligações H–Cl: 2 ´ (- 431 kJ.mol-1) = – 862
kJ
– 1830
kJ →→→ Energia
liberada
∆H°reação
= +1800 – 1830 = – 30 kJ.mol-1
|
Variação da Entalpia de Reação com a Temperatura
|
|
As entalpias absolutas dos reagentes e produtos aumentam com
a temperatura. Mas como fica o valor de ∆H em
temperatura mais alta?
Normalmente pode-se calcular o valor ∆H°m a
298 K.
1) Na
figura acima, observa-se:
– Se a capacidade calorífica dos reagentes é maior que a dos
produtos a entalpia dos reagentes crescerá mais abruptamente
com o aumento da temperatura. Se a reação for exotérmica,
como na figura, o ∆H°
de reação (∆Hr°) ficará
mais negativo.
Vamos ver outros casos:
2) Reação
Exotérmica, mas a entalpia dos reagentes (Hreagentes)
cresce menosabruptamente
que a entalpia dos produtos (Hprodutos),
pois Cp,
m (reagentes) < Cp,
m (produtos).
∆Hr°
em T2 fica menos negativo.
3) Reação
Endotérmica, mas a entalpia dos reagentes (Hreagentes)
cresce maisabruptamente
com a temperatura que a entalpia dos produtos (Hprodutos),
pois Cp, m (reagentes) > Cp,
m (produtos).
∆Hr° fica menos positivo
em T2.
4) Reação
Endotérmica, mas a entalpia dos reagentes (Hreagentes)
cresce menosabruptamente
com a temperatura que a entalpia dos produtos (Hprodutos),
pois Cp,
m (reagentes) < Cp,
m (produtos).
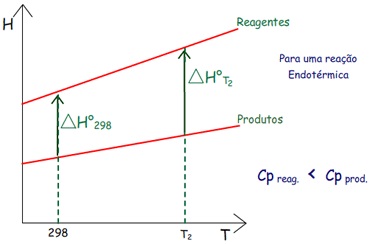 |
∆Hr° fica mais positivo
em T2.
Pode-se demonstrar para uma reação genérica:
a A + b B → c C + d D
que: ∆H°m (T2)
= ∆H°m (298
K) + (T2 - 298,15 K) . ∆CP
onde: ∆CP
= CP (produtos)
– CP (reagentes)
∆CP
= [ c CP,
m (C) + d CP,
m (D) ] –
[ a CP,
m (A) + b CP,
m (B) ]
sendo: CP,
m a capacidade calorífica molar da respectiva
substância.
Mas como a diferença de capacidade calorífica dos reagentes
e produtos é normalmente pequena, na maior parte dos casos a
entalpia de reação varia muito pouco com a temperatura. Para
pequenas diferenças de temperatura, ∆Hreação pode
ser considerada constante para todos os efeitos práticos.
∆Hr° (T2) » ∆Hr°298 → Se T2 não
for muito diferente de 298,15 K
Exemplo:
A entalpia molar (logo, se refere à formação de um mol de
amônia) da reação:
N2 (g) + 3 H2 (g) → 2 NH3
(g)
é – 92,22 kJ.mol-1 a
298 K. A síntese industrial ocorre a 450 ºC. Qual é a
entalpia padrão de reação nesta temperatura?
Resolução:
Se, ∆H°298
= – 92,22 kJ.mol-1, este valor corresponde à
reação:
1/2 N2 (g) + 3/2 H2 (g) →
NH3 (g)
|
∆CP = CP.m (NH3
(g)) – |
[ 1/2 CP
m (N2
(g)) + |
3/2 CP
m (H2
(g)) ] |
|
↓ |
↓ |
↓ |
|
∆CP =
35.06 J. K-1. mol-1
– |
[ 1/2 × 29,12 J . K-1. mol-1
+ |
3/2 × 28,82 J. K-1. mol-1] |
|
∆CP =
35.06 J. K-1
– [ 14,56 J. K-1
+ 3/2 × 28,82 J. K-1 ] |
|
∆CP =
35.06 J. K-1
– 57,79 J. K-1 |
|
∆CP =
– 22,73 J. K-1 para
cada mol de NH3 (g) formado. |
T2 = 450 + 273 = 723 K
∆H°m (T2)
= ∆H°m (298
K) + (T2 – 298 K) . ∆CP
∆H°m (450
ºC) = - 92,22 kJ. mol-1 +
[(723 K - 298 K) x (- 22,73 × 10-3 kJ.K-1.mol-1)]
∆H°m (450
ºC) = - 92,22 kJ. mol-1
+ [(425 K) x ( - 22,73 × 10-3
kJ. K-1.mol-1)]
∆H°m (450
ºC) = - 92,22 kJ. mol-1
- 9,6 kJ. mol-1)
∆H°m (450
ºC) = - 101,88 kJ. mol-1 |
Entropia
|
|
Entropia (S) é uma função de estado e para entender
o seu significado, dois fenômenos simples são analisados:
a) resfriamento
de um bloco de metal quente
b) expansão
de um gás ocupando todo o volume disponível
a) O
resfriamento ocorre porque a energia dos átomos que vibram
vigorosamente tende a se espalhar pela vizinhança. A mudança
inversa não é observada porque é muito improvável que a
energia seja recolhida da vizinhança e concentrada no
pequeno bloco de metal.
b) A
expansão ocorre porque as moléculas do gás se movem
aleatoriamente e se espalham por todo o recipiente. É também
improvável que o movimento aleatório leve todas elas para
uma parte do recipiente.
A tendência que se observa nestes processos é que a energia
e a matéria tendem a ficar mais desordenadas.
Na linguagem da termodinâmica a idéia de desordem e
aleatoriedade é expressa através da Entropia
(S).
Então: “A Entropia
(S) é
uma Função
de Estado que
mede o grau de desordem”.
Quanto menor
a desordem, menor a entropia e quanto
maior a desordem, maior a entropia.
Da mesma forma que a entalpia (H) e a energia
interna (E), a entropia (S) é função de
estado e ∆S só
depende do Estado Final e do Estado Inicial.
∆S = Sfinal – Sinicial
Como medir ∆S?
Exemplo:
Cristal de CO a T =
0 K
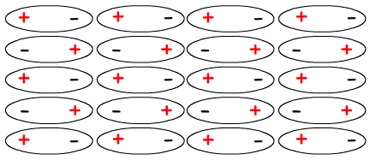 |
O CO é uma molécula polar e a 0 K todos os
dipolos estão perfeitamente alinhados.
|
Ordem perfeita |
} S=
0 |
|
Desordem nula |
|
Cristal de CO a T > 0
K
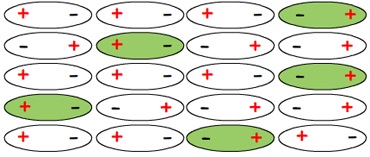 |
Ao se fornecer calor ao cristal e eleva sua T, o
movimento térmico das moléculas (vibrações)
dentro da rede faz com que alguns dipolos
troquem a sua orientação.
|
Ordem diminui |
} S> 0 |
|
Desordem aumenta |
|
Resultado:
Com o aumento de T,
menos ordem (mais desordem) é obtida → A
entropia do cristal aumenta → Com
o aumento da energia vibracional, uma estrutura mais
desordenada é mais provável.
a) Quanto
mais calor for fornecido ao sistema, maior será a extensão
do aumento da desordem produzida.
Logo: ∆S a qfornecido
b) Quanto
mais alta for a temperatura do sistema, menor será a
extensão do aumento provocado por uma certa quantidade de
calor, pois o sistema já está mais desordenado.
Ou seja: uma certa quantidade de calor (q) provoca
menor ∆S a
altas T (sistema
mais desordenado). É como avaliar o impacto de um espirro em
um ambiente silencioso (biblioteca) ou em um ambiente
barulhento (discoteca).
Logo: ∆S a 1/T
em que “q” foi fornecido.
Desta forma, pode-se demonstrar que, se a temperatura for
constante, a variação de entropia (∆S)
de um sistema pode ser calculada por:
∆S = qrev / T
Unidade de S:
J. K-1
ou cal. K-1
onde: qrev =
energia transferida reversivelmente
T
= temperatura absoluta na qual ocorre a transferência de
energia
Em uma transferência reversível de energia, na forma de
calor, as temperaturas, da vizinhança e do sistema, são
infinitesimalmente diferentes.
OBS: Apesar da Entropia ser Função de Estado, ∆S,
deve sempre ser calculado considerando processos
reversíveis, assim como ∆H é
igual a“q” somente se “q = qP”
e ∆E é
igual a“q” somente se “q = qV”,
embora H e E sejam
Funções de Estado. |
Energia Livre de Gibbs (G) – 2º Princípio da Termodinâmica
– Espontaneidade de Reações Químicas
|
|
O primeiro princípio da termodinâmica, diz que SE uma
transformação ocorre, a energia total do universo (sistema
+ vizinhança) permanece inalterada.
O primeiro princípio não trata da questão do que está por
trás do SE.
Por que algumas transformações ocorrem e outras não?
#
A água flui montanha abaixo naturalmente, mas é preciso
bombeá-la para levá-la montanha acima.
#
O calor passa de um corpo quente para um corpo frio
espontaneamente e para inverter o processo é preciso a
intervenção de uma bomba de calor ou de um refrigerador.
#
O ferro enferruja naturalmente, mas a ferrugem para ser
convertida em ferro (obtenção de ferro a partir de seus
minérios), exige intervenção humana.
Em se tratando de reações químicas, quando se questiona se
uma reação química avança numa dada direção, conforme a
indicação de uma equação química, na verdade se quer saber
se a reação é espontânea naquela direção.
O primeiro princípio não fornece a resposta.
As reações químicas endotérmicas (∆H >
0) foram um quebra cabeças para os químicos do século XIX,
que acreditavam que as reações só poderiam ocorrer se
houvesse decréscimo de energia do sistema. No entanto, estes
eram obrigados a se render ao fato de existiam muitas
reações endotérmicas que eram espontâneas.
O segundo princípio da termodinâmica responde às perguntas
sobre espontaneidade de uma reação química e este segundo
princípio se exprime em termos da Função de
Estado Termodinâmica, Entropia.
O segundo princípio da termodinâmica pode ser enunciado
como:
“A Entropia de um sistema isolado aumenta no decorrer de
qualquer processo espontâneo”.
Assim:
# O
resfriamento do metal quente é acompanhado de aumento de
entropia, quando a energia se espalha pela vizinhança. Neste
caso, o “sistema isolado” é o “Universo” (sistema (bloco)
+ vizinhança).
# A
expansão de um gás é acompanhada de aumento de entropia,
quando as moléculas se espalham aleatoriamente por todo o
recipiente.
Então: A direção natural do Universo é ir da “Ordem”
para a “Desordem”, ou seja, da menor para a
maior “Entropia”.
OBS: Para medidas experimentais, um pequeno sistema isolado,
como uma garrafa isolada termicamente ou um calorímetro,
pode representar o Universo.
| |
↓
|
|
| |
Sistema Isolado → |
Universo |
∆Suniv. = (∆Ssistema
+ ∆Svizinhança)
> 0
A entropia,
portanto, é bem diferente da energia:
#
A energia não
pode ser criada nem destruída numa transformação química
(Princípio da Conservação da Energia).
#
A entropia sempre
aumenta em uma transformação espontânea, portanto a
entropia é criada em um processo natural.
Como o critério para espontaneidade é
o aumento da
entropia total e
não o decréscimo da energia do sistema, fica esclarecido o
problema das reações endotérmicas.
| Num processo endotérmico: ∆Svizinança <
0 |
| |
↓ |
|
| calor flui: vizinhança → sistema |
Mas:
∆Ssistema precisa
ser positivo e ser suficientemente grande para ∆Suniv >
0.
∆Ssistema = ∆S devido
ao fluxo de calor + entropia criada
Logo: ∆Ssistema
> | ∆Svizinhança | → ∆Suniv >
0
+
–
Conclusão: Reações Endotérmicas espontâneas são
comandadas pelo aumento dominante da desordem do sistema.
Exemplo: Gelo funde espontaneamente acima de 0 ºC e 1 atm.
∆H > 0 → fusão
absorve calor
∆Svizinhança <
0 → vizinhança
perde calor
∆Ssistema >
0 → água
líquida é mais desordenada que o gelo
∆Ssistema > ∆Svizinhança
para ∆Stotal
> 0
∆Ssistema +
devido ao ganho de calor + Entropia criada
∆Svizinhança –
devido a perda de calor
Resumindo:
1) Processo espontâneo: ∆Ssistema ≠ – ∆Svizinhança → ∆Stotal >
0
2) Processo em equilíbrio: ∆Ssistema =
– ∆Svizinhança → ∆Stotal =
0
Fazendo-se um tratamento matemático pode-se fazer uma
avaliação através do sistema:
∆Stotal = ∆Ssistema
+ ∆Svizinhança
Mas: ∆Svizinhança
= qrev./ T
Imaginando que a vizinhança é tão grande que a temperatura e
a pressão permanecem constantes, tem-se:
qrev. vizinhança = qp
= – qp
sistema = – ∆Hsistema
Logo: ∆Svizinhança
= – ∆Hsistema / T
(a P e T constante)
Substituindo: ∆Stotal = ∆Ssistema
+ (– ∆Hsistema / T)
Modificando a expressão se obtém:
T ∆Stotal
= T ∆Ssistema
– ∆Hsistema)
ou
| T ∆Stotal
= |
– (∆Hsistema
– T ∆Ssistema) |
| + + |
↓ |
| |
– |
Para: ∆Stotal
> 0 → T ∆Stotal
> 0
E: (∆Hsistema – T ∆Ssistema)
< 0 → para
processos espontâneos
OBS: Sempre que o subscrito das Funções de Estado são
omitidos, as mesmas se referem ao sistema.
Logo: Em transformações espontâneas a T e P constantes:
∆H – T ∆S
< 0
É bastante conveniente, então, definir uma nova Função de
Estado em termos de H e S que
seja diretamente útil como critério de espontaneidade.
Para isto o físico americano Josiah Willard Gibbs introduziu
o conceito de Energia Livre (G), também conhecida
como Energia
Livre de Gibbs:
G = H
– T . S
G é uma
Função de Estado e em química só usamos variações de G (∆G)
e não o seu valor absoluto. Em processos que ocorrem a T e P constante
se tem:
Pode-se perceber que: ∆G
= – T . ∆Stotal
(a T e P constante)
Logo: Em processos espontâneos a T e P constante: ∆G
< 0
Ou seja, a direção do processo espontâneo é a direção da
diminuição da Energia Livre.
OBS: A grande importância da introdução do conceito de
energia livre é que, se a pressão e a temperatura permanecem
constante pode-se predizer se um processo é espontâneo
somente em termos das propriedades termodinâmicas do
sistema.
As variações de entalpia e entropia numa reação química,
dependem dos reagentes e produtos e podem ser positivas ou
negativas.
Estas variações determinam o sinal da variação de Energia
Livre e dizem se a reação é favorável aos produtos
(espontânea) ou aos reagentes (não espontânea).
A tabela abaixo sistematiza estas informações:
|
∆H |
∆S |
Processo Espontâneo? |
| Exotérmico (∆H < 0) |
S ↑ (∆S
> 0) |
Sim, ∆G
< 0 (sempre) |
| Exotérmico (∆H < 0) |
S ↓ (∆S
< 0) |
Sim, quando:
|T . ∆S|
< |∆H| → ∆G
< 0Espontâneo para T abaixo de um certo valor. |
| Endotérmico (∆H > 0) |
S ↑ (∆S
> 0) |
Sim, quando:
T . ∆S
> ∆H → ∆G
< 0Espontâneo para T acima de um certo valor. |
| Endotérmico (∆H > 0) |
S ↓ (∆S
< 0) |
Não → ∆G
> 0 (sempre) |
Pode-se perceber que quando ∆H
e ∆S
tem o mesmo sinal, a temperatura do processo é fundamental
na determinação da espontaneidade ou não do mesmo.
Exemplo:
1) Solidificação da
água a 1 atm:
|
∆H < 0 (exotérmico) |
} |
para T
< 273 K (0 ºC) |
∆G < 0 |
|
∆S < 0 (diminui a
desordem: Sgelo
< Ságua) |
para T
> 273 K (0 ºC) |
∆G > 0 |
| |
|
|
↓
|
| |
|
Processo não espontâneo
|
2) Vaporização da
água a 1 atm:
|
∆H > 0
(endotérmico) |
} |
para T >
373 K (100 ºC) |
∆G <
0 |
|
∆S > 0 (aumenta a
desordem: Svapor
> Ságua) |
para T <
373 K (100 ºC) |
∆G > 0 |
| |
|
|
↓
|
| |
|
Processo não espontâneo
|
|
|
Energia Livre e Trabalho Útil Máximo |
|
Uma das aplicações mais importantes das reações químicas é a
produção de energia sob a forma de trabalho útil (ou
trabalho não expansivo)
A variação de energia
livre de um
processo permite a predição do trabalho útil máximo ou
trabalho não expansivo máximo que um processo pode realizar
quando a temperatura e a pressão são constantes
O trabalho útil, ou não expansivo, é qualquer tipo de
trabalho que não seja devido à expansão contra uma pressão.
Inclui trabalho elétrico, trabalho mecânico que não seja de
expansão, trabalho de atividade muscular, trabalho de enviar
sinais nervosos através dos neurônios, etc.
O trabalho elétrico, trabalho de empurrar elétrons em um
circuito elétrico é a base da geração química de energia
elétrica, que através de baterias acionam equipamentos
eletrônicos: celulares, computadores, etc.
O trabalho mecânico não expansivo pode ser o alongamento de
uma mola ou a elevação de um peso ladeira acima, por
exemplo. A combustão da gasolina viabiliza o deslocamento de
um automóvel – é uma reação química gerando trabalho
mecânico.
OBS: Ao se obter trabalho de um processo, trabalho tem sinal
negativo (w <
0), pois energia abandonou o sistema sob forma de trabalho.
Somente é possível obter trabalho de um processo, se o sinal
de ∆G também
for negativo (∆G <
0).
MAS: O conceito de trabalho máximo útil de uma reação
química é uma idealização.
Em qualquer situação real, a quantidade de trabalho obtido é
menor que o máximo previsto por ∆G provocando aumento
da entropia da vizinhança.
POIS:
wmáximo = wreversível
E
|
wreversível
|
>
|
wirreversível
|
|
↓
|
|
↓
|
|
Processo
|
|
Processo
|
|
em equilíbrio
|
|
irreversível (espontâneo)
|
Isto ocorre porque os processos reais são sempre
irreversíveis e o trabalho máximo útil somente pode ser
extraído de uma transformação reversível.
Por isso a definição:
“A variação de energia
livre de um
processo é igual ao trabalho máximo útil (ou de não
expansão) que o sistema pode realizar
em temperatura e pressão constante, ou seja, a quantidade
máxima de energia produzida pelo processo que pode ser
teoricamente aproveitada como trabalho, a temperatura e
pressão constante." |
|
Entropia Padrão Absoluta – 3º Princípio da Termodinâmica |
|
O terceiro princípio da termodinâmica afirma:
“Uma substância pura perfeitamente cristalina a 0 K tem
entropia nula nesta temperatura.”
Este princípio faz sentido, pois no zero absoluto de
temperatura a ordem é perfeita para um cristal puro. Mas
quando a temperatura se eleva, a substância fica mais
desordenada pela absorção de calor e a entropia aumenta.
Pode-se determinar a entropia de uma substância pura a uma
temperatura diferente de 0 K, por exemplo 298 K (25 ºC),
pelo aquecimento lento desta substância de 0 K a 298 K.
O valor de ∆S (variação
de entropia) quando há aquecimento na temperatura T é:
qrev / T = ∆S
Supondo aquecimento muito lento de :
| |
0 K a 2,0 K →
|
supondo que qabs =
0,19 J
|
}
|
∆S =
0,19 J / 1 K =
|
0,19 J . K-1
|
| |
|
Tmédio =
1,0 K
|
| |
|
|
|
|
↓ |
| |
|
|
|
|
Entropia a 2,0
K
|
| |
2,0 K a 4,0 K →
|
supondo que qabs =
0,88 J
|
}
|
∆S =
0,88 J / 3 K =
|
0,29 J . K-1
|
| |
|
Tmédio =
3,0 K
|
| |
|
|
|
|
↓ |
| |
|
|
|
Entropia a 4,0
K =
0,19 + 0,29 =0,48 J . K-1
|
| |
4,0 K a 6,0 K →
|
supondo que qabs =1,86
J
|
}
|
∆S =1,86
J / 5 K =
|
0,37 J . K-1
|
| |
|
Tmédio =
5,0 K
|
| |
|
|
|
|
↓ |
| |
|
|
Entropia a 6,0
K =
0,19 + 0,29 + 0,37 = 0,85
J . K-1
|
Procedendo-se desta maneira, pode-se calcular a entropia da
substância pura a 298 K.
A entropia aumenta
gradualmente quando a temperatura se eleva. Quando ocorre
mudança de fase (S → L ....ou.... L → G),
a entropia aumenta
descontinuamente. O valor de ∆S na
mudança de fase é:
∆Smudança de fase = ∆H mudança
de fase / Tmudança
de fase
A figura abaixo ilustra como varia a entropia de uma
substância que está no estado gasoso a 298 K, quando a
temperatura varia de 0 K a 298 K
Define-se entropia
padrão absoluta molar (S°m)
de uma substância pura como o valor da entropia de 1 mol
desta substância pura no estado padrão (P = 1 atm, a uma
dada temperatura que normalmente é 298 K).
Os valores de S°m,
298 de
substâncias puras são tabelados e representam todo o aumento
da entropia que a substância acumulou com o aquecimento de 0
K a 298 K.
OBS: Os valores de S°m,
298 são sempre positivos, pois a Entropia sempre
aumenta com a temperatura.
Exemplo: Tabela com valores de S°m,
298 (J. K-1. mol-1)
|
Substância |
S°m, 298 |
Substância |
S°m, 298 |
Substância |
S°m, 298 |
|
Gases |
Líquidos |
Sólidos |
|
Amônia, NH3 |
192,4 |
Benzeno, C6H6 |
173,3 |
Óxido de cálcio, CaO |
39,8 |
|
Dióxido de carbono, CO2 |
213,7 |
Etanol, C2H5OH |
160,7 |
Carbonato de cálcio, CaCO3 |
92,9 |
|
Hidrogênio, H2 |
130,7 |
Água, H2O |
69,9 |
Diamante, C |
2,4 |
|
Nitrogênio, N2 |
191,6 |
|
|
Grafita, C |
5,7 |
|
Oxigênio, O2 |
205,1 |
|
|
Chumbo, Pb |
64,8 |
ATKINS, P., JONES, L., Princípios
de química: questionando a vida moderna e o meio
ambiente. 3. ed. Porto Alegre: Bookman, 2006.
p.337.
|
Variação
de Entropia numa Reação Química
|
|
Dispondo-se das entropias padrão absolutas molares a 298 K
de todas as substâncias numa reação química, pode-se
calcular a variação de entropia (∆S°m,
298) para a reação a 298 K através da expressão:
|
∆Sr°m,
298 = Σ Sr°m,
298 (produtos)
– Σ Sr°m,
298 (reagentes) |
Exemplo:
Para calcular-se a variação de entropia a 298 K na reação de
formação de amônia a partir de N2 (g) e
H2 (g).
N2 (g) + 3 H2 (g) → 2
NH3 (g)
∆Sr° 298
= ( 2 x S°m,
298 (NH3
(g)) – [S°m, 298 (N2
(g)) +(3 x S°m,
298 (H2
(g))]
|
Dados da tabela: |
S°m, 298 (NH3
(g)) = 192,4 J. K-1. mol-1
|
| |
S°m, 298 (N2
(g)) = 191,6 J. K-1. mol-1
|
| |
S°m, 298 (H2
(g)) = 130,7 J. K-1. mol-1
|
∆Sr° 298
= (2 x 192,4)
– [191,6 + 3 x 130,7]
∆Sr° 298
= – 198,9 J. K-1
OBS: Apesar do valor da entropia
padrão absoluta molar de
uma substância (S°m, 298) ser sempre
positivo, os valores da variação
de entropia de uma reação química (∆Sr° 298)
podem ser negativos quando os produtos têm menor desordem
que os reagentes.
Mesmo sem conhecer os valores de entropia padrão absoluta
molar das substâncias, é possível às vezes prever o sinal de ∆Sr°.
A entropia usualmente cresce nas seguintes situações:
1) Reação
em que uma molécula se divide em duas ou mais moléculas
pequenas.
2) Reação
em que há aumento do número de mols gasosos.
3) Processo
em que um sólido se transforma em líquido ou gás, ou em que
líquido se transforma em gás.
Exemplos:
|
a) C6H12O6
(s) → 2
C2H5OH(ℓ)
+ 2 CO2 (g) |
(∆S > 0)
|
|
b) CaCO3 (s) → CaO (s)
+ CO2 (g) |
(∆S > 0)
|
|
c) CS2(ℓ) → CS2
(g) |
(∆S > 0)
|
|
d) 2 Hg(ℓ)
+ O2 (g) → 2
HgO(s) |
(∆S < 0)
|
|
e) 2 Na2O2 (s)
+ 2 H2O(ℓ) → 4
NaOH (aq)
+ O2 (g) |
(∆S > 0)
|
|
f) 2 NH3 (g) + CO2
(g) → NH2CONH2
(aq) + H2O(ℓ) |
(∆S < 0)
|
|
g) CO (g)
+ 2 H2 (g) → CH3OH(ℓ) |
(∆S < 0)
|
|
h) K (s)
+ H2O(ℓ) → KOH (aq)
+ ½ H2 (g) |
(∆S > 0)
|
|
|
Energia Livre Padrão Molar de Formação (∆Gf°m) |
|
Energia Livre Padrão Molar de Formação (∆Gf°m)
de uma substância se define de maneira análoga à Entalpia
Padrão Molar de Formação.
∆Gf°m é
a variação de
energia livre que
ocorre quando 1 mol de substância, no estado
padrão (P = 1
atm) é formado a partir dos seus elementos também no estado
padrão, em um certo valor de temperatura (comumente 298 K).
Da mesma forma que: ∆Hf°m de
substâncias simples são nulos, os valores de ∆Gf°m de
substâncias simples também são nulos.
| Exemplo: |
∆Gf°m (O2
(g)) = 0 |
| |
∆Gf°m (C (grafita))
= 0 |
| |
∆Gf°m (Hg (ℓ) )
= 0 |
A partir dos valores de ∆Hf°m,
298 e S°m,
298, é possível calcular os valores de ∆Gf°m ,
298os quais também são tabelados.
Exemplo:
Para calcular-se ∆Gf°m ,
298 de Fe2O3
(s).
Lembrando-se a relação ∆G = ∆H – T. ∆S,
utiliza-se a reação de formação da substância e os valores
tabelados de ∆Hf°m,
298 e S°m,
298
2 Fe (s) +
3/2 O2 (g) → Fe2O3
(s)
| Dados da tabela: |
∆Hf°m,
298 (Fe2O3
(s)) = – 824,20 kJ. mol-1 |
| |
S°m, 298 (Fe2O3
(s)) = 87,40 J. K-1. mol-1 |
| |
S°m, 298 (O2 (g))
= 205,14 J. K-1. mol-1 |
| |
S°m, 298 (Fe (s))
= 27,28 J. K-1. mol-1 |
∆Sf°m, 298 (Fe2O3)
= S°m,
298 (Fe2O3
(s)) – [2 x
S°m, 298 (Fe (s))
+ 3/2 S°m,
298 (O2 (g))]
∆Sf°m, 298 (Fe2O3)
= 87,40 – [2 x 27,28 + 3/2 x 205,14]
∆Sf°m, 298 (Fe2O3)
= 87,40 – [54,56 + 307,71]
∆Sf°m, 298 (Fe2O3)
= 87,40 – 362,27
∆Sf°m, 298 (Fe2O3)
= – 274,87 J. K-1. mol-1
∆Gf°m, 298 = ∆Hf°m,
298 – 298 x ∆Sf°m,
298
∆Gf°m, 298 =
– 824,20 kJ. mol-1 –
298 K x (– 274,87 J. K-1. mol-1)
∆Gf°m, 298 =
– 824,20 kJ. mol-1 –
298 K (–
274,87 x 10-3 kJ . K-1. mol-1)
∆Gf°m, 298 =
– 824,20 kJ. mol-1 –
(– 81,91 kJ. mol-1)
∆Gf°m, 298 =
– 824,20 kJ. mol-1 +
81,91 kJ. mol-1
∆Gf°m, 298 =
– 742,29 kJ. mol-1
Exemplo: Tabela com valores de ∆Gf°m,
298 (J. K-1. mol-1) |
|
Cálculo de Energia Livre Padrão de Reação a 298 K (∆Gr°298) |
|
a) A
partir de ∆H°298 e ∆S°298
Pode-se calcular ∆Gr°298 através
da Equação:
-
|
∆Gr°298 = ∆Hr°298 –
298 K . ∆Sr°298 |
Exemplo: Calcular ∆Gr°298 para
a combustão de 1 mol de glicose a 298 K.
C6H12O6 (s) +
O2 (g) → 6
CO2 (g) +
6 H2O (ℓ)
| Dados da tabela: |
∆Hf°m,
298 (glicose)
= – 1268 kJ. mol-1 |
| |
∆Hf°m,
298 (CO2
(g)) = – 393,5 kJ. mol-1 |
| |
∆Hf°m,
298 (H2O (ℓ))
= – 285,83 kJ. mol-1 |
| |
S°m, 298 (glicose)
= 212 J. K-1. mol-1 |
| |
S°m, 298 (O2
(g)) = 205,14 J. K-1. mol-1 |
| |
S°m, 298 (CO2
(g)) = 213,74 J. K-1. mol-1 |
| |
S°m, 298 (H2O (ℓ))
= 69,91 J. K-1. mol-1 |
| Cálculo de ∆Hr298: |
|
| |
∆Hr°298= Σ ∆Hf°m,
298 (Produtos) – Σ ∆Hf°m,
298 (Reagentes) |
| |
∆Hr°298 =
[ 6 x ∆Hf°m,
298 (CO2
(g)) + 6 x ∆Hf°m,
298 (H2O (ℓ))
] – ∆Hf°m,
298 (glicose) |
| |
∆Hr°298 =
[ 6 x (– 393,51) + 6 x (– 285,83) ]
– (– 1268) |
| |
∆Hr°298 =
(– 2361,06) + (– 1714,98) + 1268 |
| |
∆Hr°298 =
– 2808,04 kJ. mol-1 |
| Cálculo de ∆Srr°298: |
|
| |
∆Sr°298= Σ Sf°m,
298 (Produtos) – Σ Sf°m,
298 (Reagentes) |
| |
∆Sr°298 =
[ 6 x Sf°m,
298 (CO2
(g)) + 6 x Sf°m,
298 (H2O (ℓ))
] – [Sf°m,
298 (glicose)
+ 6 x Sf°m,
298 (O2
(g)) ] |
| |
∆Sr°298 =
[ 6 x 213,74 + 6 x 69,91 ] – [212 +
6 x 205,14] |
| |
∆Sr°298 =
[ 1282,44 + 419,46 ] – [212 +
1230,84] |
| |
∆Sr°298 =
1701,19 – 1442,84 |
| |
∆Sr°298 =
259,06 J . K-1 . mol-1 |
| – Cálculo de∆Gr°298: |
|
| |
∆Gr°298= ∆Hf°m,
298 –
298 K . ∆Sr°298 |
| |
∆Gr°298= –
2808,04 kJ. mol-1 –
298 K x
259,06 J. K-1.mol-1 |
| |
∆Gr°298=–
2808,04 kJ. mol-1 –
298 K x
259,06 10–3 kJ.K-1. mol-1 |
| |
∆Gr°298=
– 2808,04 kJ. mol-1 –
77,2 kJ. mol-1 |
| |
∆Gr°298=
– 2885,24 kJ. mol-1 |
b) A
partir de ∆Gf°m,
298
Pode-se calcular ∆Gr°298
a partir de:
-
|
∆Gr°298 = Σ ∆Gf°m,
298 (Produtos) – Σ ∆Gf°m,
298 (Reagentes) |
Exemplo: Utilizando-se o mesmo exemplo
anterior, ou seja,
Calcular ∆Gr°298 para
a combustão de 1 mol de glicose a 298 K.
C6H12O6 (s) +
O2 (g) → 6
CO2 (g) +
6 H2O (ℓ)
| Dados da tabela: |
∆Gf°m,
298 (glicose)
= – 910 kJ. mol-1 |
| |
∆Gf°m,
298 (O2
(g)) = zero |
| |
∆Gf°m,
298 (CO2
(g) )
= – 394,36 kJ. mol-1 |
| |
∆Gf°m,
298 (H2O(ℓ))
= – 237,13 J. K-1. mol-1 |
∆Gr°298 =
[6 x ∆Gf°m,
298 (CO2
(g) ))
+ 6 x ∆Gf°m,
298 (H2O (ℓ))
] – ∆Gf°m,
298 (glicose)
∆Gr°298 =
[ 6 x (– 394,36) + 6 x (– 237,13) ] – (–
910)
∆Gr°298 =
[ (– 2366,16) + (– 1422,78) ] – (– 910)
∆Gr°298 =
[ – 3788,94 ] – (– 910)
∆Gr°298 =
– 2878,94 kJ. mol-1
|
|
Efeito da Temperatura sobre Energia Livre Padrão (∆G°) |
|
Já foi visto que os valores de ∆H°
de reação não variam muito com a temperatura.
Da mesma forma, os valores de ∆S°
de reação variam muito pouco com a temperatura. As entropias
dos reagentes e produtos são afetadas pelo aumento de
temperatura, mas a diferença entre eles muda muito pouco.
Para todos os efeitos práticos, pode-se considerar que ∆Hr°
e ∆Sr°
variam muito pouco com a temperatura.
Mas ∆Gr°
depende da temperatura, pois:
Exemplo: Calcular ∆Gr°
para a combustão de 1 mol de glicose a 85 ºC.
Foi visto no exemplo anterior para esta reação
∆Hr°298 =
– 2808,04 kJ. mol-1
∆Sr°298 =
259,06 J. K-1. mol-1
∆Gr°298 =
– 2885,24 kJ. mol-1
T = 85 ºC = 358 K
∆Gr°358 =
– 2808,04 kJ. mol-1 –
358 K x 259,06 J. K-1. mol-1
∆Gr°358 =
– 2808,04 kJ. mol-1 –
358 K x
259,06 10–3 kJ. K-1. mol-1
∆Gr°358 =
– 2808,04 kJ. mol-1 –
92,743 kJ. mol-1
∆Gr°358 =
– 2900,78 kJ. mol-1
|
∆Gr°298 =
– 2878,94 kJ. mol-1 ↔ ∆Gr°358 =
– 2900,78 kJ. mol-1 |
∆Gr° pode inclusive mudar de sinal
quando a temperatura se altera.
No caso de uma reação exotérmica (∆Hr°
< 0) com uma entropia de reação negativa (∆Sr°
< 0), o termo (– T. ∆Srº)
contribui como um termo positivo para ∆Gr°.
Em uma reação desse tipo ∆Gr°
será negativo em T baixas,
mas pode se tornar positivo em T altas.
No caso de uma reação endotérmica (∆Hr°
> 0) com uma entropia de reação positiva (∆Sr°
> 0), o termo ∆Hr°
contribui como termo positivo no cálculo ∆Gr°.
Em uma reação desse tipo∆Gr°
será negativo em T altas,
mas pode se tornar positivo em T baixas.
Já foi visto que se ∆Hr°
> 0 e ∆Sr°
< 0 a reação nunca será espontânea pois ∆Gr°
será positivo em qualquer temperatura.
Mas no caso de ∆Hr°
< 0 e ∆Sr°
> 0 a reação será espontânea em qualquer temperatura pois ∆Gr°
será sempre negativo.
Como: ∆Grº = ∆Hrº
– T. ∆Srº
Logo: A temperatura em que ∆Grº =
0 é a temperatura em que uma reação troca da espontaneidade
para a não espontaneidade.
Se: ∆Grº =
0 ∆Hrº
– T. ∆Srº
= 0
E: T = ∆Hrº / ∆Srº
Temperatura em que ∆Grº muda
de sinal.
Exemplo:
Estimar a temperatura a partir da qual é termodinamicamente
possível para o carbono reduzir óxido de ferro (III) até
ferro em condição padrão, pela reação endotérmica:
2 Fe2O3 (s) +
3 C (grafita) → 4
Fe (s) +
3 CO2 (g)
| Dados da tabela: |
∆Hf°m,
298 (Fe2O3
(s)) = – 824,2 kJ. mol-1 |
| |
∆Hf°m,
298 (CO2
(g)) = – 393,5 kJ. mol-1 |
| |
S°m, 298 (Fe2O3
(s)) = 87,4 J. K-1. mol-1 |
| |
S°m, 298 (C (grafita))
= 5,7 J. K-1. mol-1 |
| |
S°m, 298 (Fe (s))
= 27,3 J. K-1. mol-1 |
| |
S°m, 298 (CO2
(g)) = 213,74 J. K-1. mol-1 |
Resolução:
∆Hr° > 0 → já
que a reação é endotérmica.
Pode-se prever que ∆Sr°
> 0, já que há um aumento da desordem pois forma-se um
produto gasoso.
Logo esta reação terá ∆Grº <
0 quando ∆Hr°
< T. ∆Srº → altas T
| – Cálculo de ∆Hr°298: |
|
| |
∆Hr°298= Σ ∆Hf°m,
298 (Produtos) – Σ ∆Hf°m,
298 (Reagentes) |
| |
∆Hr°298 =
[ 3 x ∆Hf°m,
298 (CO2
(g))] – [
2 x ∆Hf°m,
298(Fe2O3
(s))] |
| |
∆Hr°298 =
[ 3 x (– 393,51)] –[
2 x (– 824,2) ] |
| |
∆Hr°298 = [
– 1180,5 ] – [ – 1648,4 ] |
| |
∆Hr°298 = [
– 1180,5 ] + 1648,4 |
| |
∆Hr°298 = +
467,9 kJ. mol-1→ ∆Hr°
> 0 |
| Cálculode ∆Srr°298: |
|
| |
∆Sr°298= Σ Sf°m,
298 (Produtos) – Σ Sf°m,
298 (Reagentes) |
| |
∆Sr°298 =
[ 4 x S°m,
298 (Fe (s))
+ 3 x S°m,
298 (CO2
(g)) ] – [2 x S°m,298 (Fe2O3
(s)) + 3 x S°m,
298 (C (grafita))
] |
| |
∆Sr°298 =
[ 4 x 27,3 + 3 x 213,7 ] – [ 2 x 87,4 +
3 x 5,7 ] |
| |
∆Sr°298 =
[ 109,2 + 641,1 ] – [ 174,8 +
17,1 ] |
| |
∆Sr°298 =
750,3 – 191,9 |
| |
∆Sr°298 =
558,4 J . K-1 . mol-1 → ∆Sr°298 >
0 |
| – Cálculo de∆Gr°298: |
|
| |
∆Gr°298= ∆Hf°m,
298 –
298 K . ∆Sr°298 |
| |
∆Gr°298= +
467,94 kJ. mol-1 –
298 K x
558,4 J. K-1.mol-1 |
| |
∆Gr°298= +
467,9 kJ. mol-1 –
298 K x
558,4 10–3 kJ. K-1. mol-1 |
| |
∆Gr°298=
+ 467,9 kJ. mol-1 –
166,4 kJ. mol-1 |
| |
∆Gr°298=
+ 301,5 kJ. mol-1 → ∆Gr°298 >
0 |
A temperatura na qual ∆Gr°298
muda de positivo para negativo é:
|
T = ∆Hrº / ∆Srº |
T =
467,9 kJ. mol-1 /
558,4 x 10–3 kJ. K-1. mol-1 |
| |
T =
837,9 K = 564,9 ºC |
Como a reação é endotérmica, a temperatura mínima em que a
redução ocorre, em condições padrão, é cerca de 565 ºC. |
|
Energia Livre e
Equilíbrio |
|
Foi visto que a variação
da energia livre padrão (∆G°)
podia ser usada como critério
de espontaneidade de
uma reação química.
∆G° < 0 → reação
química espontânea
∆G° > 0 → reação
não espontânea
Onde: ∆G°
= G°produtos – G°reagentes
Ou seja: ∆G°
é a elevação ou diminuição da energia
livre quando
os reagentes, nos respectivos estados
padrões, se convertem completamente nos
produtos, também nos respectivos estados
padrões.
Mas: na prática não se observa freqüentemente a conversão
completa de reagentes em produtos, ou seja:
– Se ∆G°
< 0: não significa que a reação química ocorreu 100 % e
houve conversão total de reagentes em produtos → sempre
resta um pouco de reagente.
– Se ∆G°
> 0: não significa que a reação química ocorreu 0 % e que
nenhuma quantidade de produto foi formada → sempre
se forma um pouco de produto.
O que ocorre na realidade, é que:
“O sistema atinge um estado
de equilíbrio no
qual existe uma certa composição de mistura reagente +
produto com menor energia
livre.”
– Se ∆G°
< 0: Esta mistura é rica
em produtos, o que significa que a reação
avançou bastante.
– Se ∆G°
> 0: Esta mistura é rica
em reagentes, o que significa que a reação
avançou muito pouco.
Problema: A relação entre a magnitude
de ∆G° e
a composição
da mistura reagente
mais produto existente no estado
de equilíbrio.
O equilíbrio químico será estudado mais adiante, mas todos
os princípios relacionados com este assunto são da maior
importância, por que a tendência das reações químicas em
ocorrer na direção do equilíbrio é a base da maior parte da
química.
Alguns comentários breves sobre equilíbrio químico:
# Um
sistema em equilíbrio não tende a mudar em direção alguma
(direta ou inversa).
# Um
sistema permanece em equilíbrio até ser perturbado por uma
mudança de condições.
# O estado
de equilíbrio é dinâmico: os processos direto e inverso
continuam a acontecer, porém sua velocidade é a mesma: os
processos continuam a ocorrer no nível microscópico.
# Termodinamicamente,
no equilíbrio: ∆Stotal =
0 e ∆G =
0. |
|
Diagrama de Energia Livre para Reações Químicas |
|
A figura que segue, mostra qualitativamente a relação entre ∆G°
e o estado de equilíbrio. Mostra também como varia a energia
livre à medida que a reação avança:
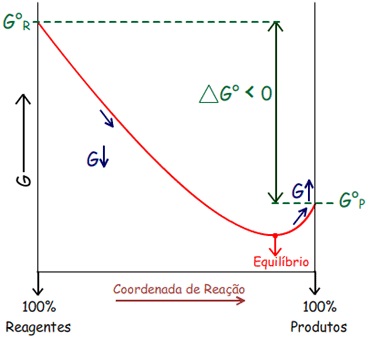 |
|
∆G° < 0 |
|
Mistura em equilíbrio
rica em produtos |
 |
|
Grande conversão de
reagentes em produtos |
|
Observa-se: A reação ocorre enquanto a energia livre do
sistema estiver decrescendo (∆G<
0). Quando a reação chegar no ponto a partir do qual a
formação de produtos implique em aumento da energia livre (∆G >
0), a reação cessa macroscópicamente e o sistema estará em
equilíbrio.
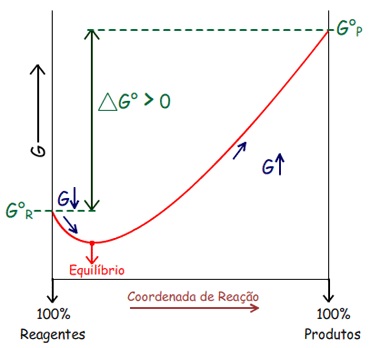 |
|
∆G° > 0 |
|
Mistura em equilíbrio
rica em reagentes |
 |
|
Pequena conversão de
reagentes em produtos |
|
Caso particular
Os gráficos anteriores permitem fazer uma distinção muito
importante entre ∆G°
e ∆G:
# ∆G°
é simplesmente G°P – G°R
#∆G é
a variação de energia livre em vários intervalos ao longo do
caminho da reação
∆G <
0 → reação
avança no sentido direto
∆G >
0 → reação
retrocede (avança no sentido inverso)
Os gráficos mostram que para uma reação qualquer em que
reagente e produtos estão na mesma fase, existe uma
composição de mistura reagente + produto que tem um mínimo
de energia livre que se situa abaixo tanto de G°R como
de G°P.
Como o sistema sempre busca o mínimo de energia livre, as
reações químicas sempre irão ocorrer em uma certa extensão
tanto se no início só houver reagentes puros (R → P)
ou só houver produtos puros (R → P).
# Em
cada caso a reação é acompanhada por um decréscimo
de energia livre enquanto
a reação se aproxima do estado
de equilíbrio.
Logo: ∆G para
qualquer reação em direção ao mínimo é negativo.
| Então: |
É o sinal de ∆G e
não o sinal de ∆Gº que
determina a espontaneidade. |
| |
∆Gº apenas determina a
posição do valor mínimo da curva de energia livre. |
No entanto, ainda que o valor de ∆Gº
não seja um indicador de espontaneidade, funciona como guia
de viabilidade para uma determinada reação.
# Não
vale a pena tentar obter certos produtos a partir de certos
reagentes se ∆Gº
>> 0, pois o rendimento seria muito pequeno.
Exemplo:
Sob condições padrão, seria possível obter iodo sólido
através do seguinte processo a 298 K?
2 HI (g) +
Cl2 (g) → 2
HCl (g) +
I2 (s)
| Dados da tabela: |
∆Gf°m,
298 (HCl (g))
= – 95,30 kJ. mol-1 |
| |
∆Gf°m,
298 (HI (g) )
= + 1,70 kJ. mol-1 |
Lembrando que:
∆Gr° 298 = ∆Gf°m,
298 (Produtos)– ∆Gf°m,
298 (Reagentes)
Resolução:
∆Gr° 298 =
[2 x ∆Gf°m,
298 (HCl (g))
] – [2 x ∆Gf°m,
298 (HI (g))
]
∆Gr° 298 =
[2 x (– 95,30) ] – [2 x (1,70) ]
∆Gr° 298 =
[– 190,60 ] – [3,40]
∆Gr° 298 =
– 194,00 kJ. mol-1 de
I2 (s)
Conclusão: Pelo sinal de ∆G°,
pode-se concluir que a posição do equilíbrio favorece a
formação de I2 (s) e,
portanto, a reação é viável. |
| |
Diagrama de Energia Livre para Mudanças de Fase
|
|
Os processos de mudança de fase são processos físicos e
apresentam diagramas de energia livre mais simples do que os
diagramas de energia livre de reações químicas, vistos no
item anterior.
Para uma dada mudança de fase como:
H2O (ℓ) → H2O (s) (Solidificação)
O equilíbrio pode existir para uma dada pressão apenas a uma
dada temperatura particular. Para a água se: P =
1 atm, a temperatura de solidificação é 0 ºC, ou seja:
(a)
T < 0 ºC: H2O (ℓ) → H2O (s) (Solidificação)
(b)
T = 0 ºC: H2O (ℓ) → H2O (s) (Equilíbrio
L/S)
(c)
T > 0 ºC: H2O (ℓ) → H2O (s) (Fusão)
Desta forma, os diagramas de energia livre são:
Em:
(a) A
energia livre diminui até toda a água existir como gelo.
(b) O
equilíbrio gelo/água líquida pode existir para qualquer
composição gelo/água.
(c) A
fusão é espontânea e ocorrerá até toda a água existir como
líquido.
|
|
Variação de Energia Livre Padrão e Constante de Equilíbrio
Termodinâmico |
|
Anteriormente foi visto de forma qualitativa que a posição
do equilíbrio numa reação química é determinada pelo sinal e
pela magnitude de ∆G°.
Foi visto também que a direção na qual a reação ocorre
depende da composição do sistema em relação ao mínimo da
curva de energia
livre.
Quantitativamente, é preciso que se conheça a relação entre ∆G (prognóstico
de espontaneidade) e ∆G°.
É possível demonstrar, para espécies gasosas, a relação
matemática a seguir (válida para 1 mol):
Gm – Gºm =
RT ln (P
/ Pº) para 1 mol
| Onde: |
Gm =
Energia livre molar da espécie gasosa a qualquer
pressão (em atm) |
| |
Gºm =
Energia livre molar padrão da espécie gasosa (a 1
atm) |
| |
P =
Qualquer pressão (em atm) |
| |
Pº = Pressão padrão (em atm) |
| |
T =
temperatura em K |
| |
R = Constante universal dos gases (8,314 J. mol-1. K-1) |
| Logo: |
Gm – Gºm =
RT ln
(P atm /
1 atm) |
| |
Gm – Gºm =
RT ln P |
OBS: P é adimensional.
Para “n” mols, se tem:
A equação acima será utilizada para deduzir a a relação
entre a constante de equilíbrio e ∆G°.
Considerando a reação genérica entre gases ideais:
a A (g) +
b B (g) → c
C (g) +
d D (g)
e que:
PA, PB, PC e PD =
pressões parciais dos reagentes e produtos.
Sabe-se que ∆G,
em quaisquer condições, pode ser dado por:
∆G = ΣGprodutos
– ΣGreagentes
Logo: ∆G
= [c.Gm (C)
+ d.Gm (D)]
– [a.Gm (A)
+ b.Gm (B)]
| Mas: |
c.Gm (C)
= c.Gºm (C)
+ c.RT.ln PC |
| |
d.Gm (D)
= d.Gºm (D)
+ d.RT.ln PD |
| |
a.Gm (A)
= a.Gºm (A)
+ a.RT.ln PA |
| |
b.Gm (B)
= b.Gºm (B)
+ b.RT.ln PB |
Substituindo:
∆G
= [c.Gºm (C)
+ c.RT.ln PC +
d.Gºm (D)
+ d.RT.ln PD]
– [a.Gºm (A)
+ a.RT.ln PA +
b.Gºm (B)
+ b.RT.ln PB]
Rearranjando:
|
∆G =
c.Gºm (C)
+ d.Gºm (D)
– a.Gºm (A)
– b.Gºm (B) +
|
c.RT.ln PC +
d.RT.ln PD –
a.RT.ln PA.RT.ln PB
|
|
↓
|
↓
|
|
∆G°
+
|
RT.ln (PCc . PDd / PAa . PBb)
|
|
Resultando
em: |
∆G = ∆G°
+ RT.ln Q |
Onde: Q = PCc . PDd / PAa . PBb
é o quociente de reação, é
adimensional.
Esta equação relaciona ∆G de
qualquer reação entre gases ideais com ∆G°
e as pressões
parciais de
reagentes e produtos.
Veja: Pressões Parciais (clique aqui)
Supondo
que as pressões parciais correspondem às pressões do estado
de equilíbrio, então:
∆G =
0 e Q = Keq
Para reações gasosas, Keq
= KP
= (PCc . PDd / PAa . PBb)eq
Assim: 0 = ∆G°
+ RT.ln KP
|
Ou seja: |
∆G° = – RT.ln KP |
|
Ou: |
KP = e –
(∆G° / RT) |
→ Para
reações gasosas |
Por outro lado, para espécies em solução, é possível
demonstrar a relação matemática a seguir:
Gm = Gºm
+ RT ln
(a / aº) →
para 1 mol
Onde: a =
atividade
aº =
atividade padrão = 1
OBS:
1) Para
espécies em solução, as condições padrão são estabelecidas
como condições de atividade unitária.
2) Para
soluções diluídas, atividade é aproximadamente igual à
concentração molar, ou seja, aº » 1
mol L–1.
Considerando soluções diluídas, com concentração molar igual
a “c” , a relação anterior pode ser modificada:
Gm = Gºm
+ RT ln
( c (mol L–1) / 1
(mol L–1)
)
Gm = Gºm
+ RT ln c onde c é adimensional.
Para ”n” mols: n Gm
= n Gºm
+ n RT ln c
Por analogia às reações em fase gasosa, considerando a
reação genérica ocorrendo em solução:
a A (aq)
+ b B (aq) → c
C (aq)
+ d D (aq)
É possível demonstrar que:
|
∆G = ∆G°
+ RT.ln |
([C]c [D]d /
[A]a [B]b) |
|
| |
↓ |
|
| |
Q →
|
adimensional |
Esta equação relaciona ∆G de
qualquer reação em solução aquosa com ∆G°
e as concentrações de reagentes e produtos.
Supondo que as concentrações correspondam às concentrações
do estado de equilíbrio, então:
∆G =
0 e Q = Keq
Para reações em solução:
Keq = Kc =
([C]c [D]d /
[A]a [B]b) eq
Assim:
0 = ∆G°
+ RT.ln Kc

|
Ou seja: |
∆G° = – RT.ln KC |
|
Ou: |
Kc = e –
(∆G° / RT) |
→ Para
reações em solução |
Observa-se que são obtidas as mesmas relações entre ∆G°
e Kp (para
reações gasosas) e ∆G°
e Kc (para
reações em solução).
Algumas conclusões podem ser tiradas:
|
à Se ∆G°
< 0 → |
expoente
positivo →
|
Keq >
1
|
| |
↓
|
|
| |
(PCc . PDd) eq
> (PAa . PBb)eq
|
|
| |
ou
|
|
| |
(CCc . CDd) eq
> (CAa . CBb)eq
|
|
| |
↓
|
|
| |
No
equilíbrio, a mistura reacional é rica em
produtos.
|
|
à Se ∆G°
<<<< 0 → |
Keq >>>>
1
|
|
↓
|
↓
|
|
∆G° mais negativo que
– 20 kJ
|
reação
praticamente completa, sobra muito pouco reagente
quando o equilíbrio é atingido.
|
|
à Se ∆G°
> 0 → |
expoente negativo →
|
Keq <
1
|
| |
↓
|
|
| |
(PCc . PDd) eq
< (PAa . PBb)eq
|
|
| |
ou
|
|
| |
(CCc . CDd) eq
< (CAa . CBb) eq
|
|
| |
↓
|
|
| |
No
equilíbrio, a mistura reacional é rica em
reagentes.
|
|
à Se ∆G°
>>>> 0 → |
Keq <<<<
1
|
|
↓
|
↓
|
|
∆G° mais positivo que
20 kJ
|
reação
praticamente não ocorre e forma muito pouco produto
quando o equilíbrio é atingido.
|
|
à Se ∆G°
= 0 (caso particular) → |
expoente = 0 →
|
Keq =
1
|
| |
↓
|
|
| |
(PCc . PDd) eq
= (PAa . PBb) eq
|
|
| |
ou
|
|
| |
(CCc . CDd) eq
= (CAa . CBb) eq
|
|
Para melhor entender os casos em que:
a) ∆G°
<<<< 0
|
Por exemplo: |
∆G° = – 50 kJ = – 50
000 J |
| |
K eq
= e –
(– 50.000 / 8,314 x 298) |
| |
K eq
= e 20,1810 |
| |
K eq
= 5,8 x 108 (a
298 K) (reação
quase completa) |
b) ∆G°
>>>> 0
|
Por exemplo: |
∆G° = 50 kJ = 50 000 J |
| |
K eq
= e –
( 50.000 / 8,314 x 298) |
| |
K eq
= e –
20,1810 |
| |
K eq
= 1,7 x 10–9 (a
298 K) (reação
quase não ocorre) |
Graficamente pode-se ver:
|
a) ∆G°
<<<< 0 |
b) ∆G°
>>>> 0 |
|
Escrevendo a equação, |
KP (ou Kc)
= e –
(∆G° / RT) |
|
em uma forma expandida, pois |
∆G° = ∆H°
– T ∆S°, |
|
obtém-se: |
KP (ou KC)
= e (∆S°
/ R) . e (– ∆H°
/RT) |
Pode-se compreender melhor as forças que atuam sobre as
reações químicas:
à
Quanto mais positivo ∆S° → maior Keq
à
Quanto mais negativo ∆H° → maior Keq
Desta forma, a tendência no sentido de alcançar o máximo de
caos molecular (maior entropia) contribui diretamente para a
magnitude de Keq,
assim como a tendência dos átomos em tentarem alcançar o
estado de menor energia também contribui para aumentar o
valor da Keq.
Exemplos:
1) O
dióxido de enxofre (SO2), gerado na combustão da
gasolina que contenha enxofre, é um poluente do ar. Mas
reage com o oxigênio (O2) quando passa pelo
catalisador presente no conversor catalítico do automóvel. O
produto da reação é o trióxido de enxofre (SO3),
um óxido muito ácido.
2 SO2 (g) + O2 (g) ⇌ 2
SO3 (g)
Para esta reação, ∆G°
= 140 kJ. mol-1 a
25 ºC. Calcular o valor de KP.
Resolução:
KP (ou Kc)
= e – (∆G° / RT)
KP = e –
(– 140 000 J. mol-1 /
8,314 J. mol-1. K-1 x 298 K)
KP = e 56,5
KP = 3,47 x 1024 → Reação
praticamente completa
2.a) A
reação:
N2 (g) + 3 H2 (g) ⇌
2 NH3 (g)
tem KP
= 6,9 x 102 a
25 ºC. Calcular ∆G°
a 25 ºC para esta reação.
Resolução:
∆G° = – RT.ln KP
∆G° = – 8,314 J. mol-1. K-1 x 298 K x ln
6,9 x 102
∆G° = – 16 195,12 J = 16,2
kJ →
por mol de N2 consumido
KP > 1
e ∆G°
< 0 → Equilíbrio
favorece produtos
2.b) Para
a reação anterior, calcular ∆G a
25 ºC quando as pressões parciais de N2, H2 e
NH3 forem
respectivamente: 0,5 atm, 0,1 atm e 0,2 atm.
Se o sistema não estiver em equilíbrio, em que sentido a
reação estará ocorrendo?
Resolução
∆G = ∆G°
+ RT.ln Q →
Q = (PNH3)2 /
[PN2 x (PH2)3]
∆G = – 16 195,12 J + 8,314 J. mol-1. K-1 x 298 K x ln
{(0,2)2 /
[0,5 x (0,1)3]}
∆G = – 16 195,12 + 8,314 x 298 x ln
{0,04 / 5 . 10–4}
∆G = – 16 195,12 + 8,314 x 298 x ln
80
∆G = – 16 195,12 + 8,314 x 298 x 4,3820
∆G = – 16 195,12 + 10856,786
∆G = – 5338,3335 J » –
5,3 kJ
|
∆G ≠ 0 →
Sistema fora do equilíbrio |
|
∆G < 0 →
reação ocorre espontaneamente no sentido direto, R → P,
até o equilíbrio ser atingido |
2.c) Para
a mesma reação, calcular ∆G a
25 ºC quando as pressões parciais de N2, H2 e
NH3 forem
respectivamente: 0,1 atm, 0,05 atm e 0,6 atm.
Se o sistema não estiver em equilíbrio, em que sentido a
reação estará ocorrendo?
Resolução
∆G = ∆G°
+ RT.ln Q →
Q = (PNH3)2 /
[PN2 x (PH2)3]
∆G = – 16 195,12 J + 8,314 J. mol-1. K-1 x 298 K x ln
{(0,6)2 /
[0,1 x (0,05)3]}
∆G = – 16 195,12 + 8,314 x 298 x ln
{0,36 / 1,25 . 10–5}
∆G = – 16 195,12 + 8,314 x 298 x ln
28800
∆G = – 16 195,12 + 8,314 x 298 x 10,268131
∆G = – 16 195,12 + 25440,033
∆G = + 9244,913 J » +
9,24 kJ
|
∆G ≠ 0 →
Sistema fora do equilíbrio |
|
∆G
> 0 →
reação não está ocorrendo espontaneamente no sentido
R → P,
portanto está ocorrendo no sentido inverso R ← P
até o equilíbrio ser atingido |
|
Constante de Equilíbrio Termodinâmico em temperaturas
diferente de 25ºC
|
|
Já foi visto que conhecendo ∆G°298 pode-se
calcular o valor da Keq (KP ou KC)
a 298 K.
Quando a temperatura se afasta de 25 ºC, a posição do
equilíbrio também muda devido às mudanças no valor de ∆G°T.
Portanto, é preciso calcular o valor de ∆G°T (T ≠ 298
K), para que se possa calcular o valor da Keq em
outra temperatura.
Exemplo:
O óxido nitroso (N2O) é um anestésico conhecido
como gás do riso, porque às vezes libera pacientes de suas
inibições. A decomposição do óxido nitroso tem KP =
1,8 x 1036 a
25 ºC.
2 N2O (g) ⇌
2 N2 (g) + O2 (g)
Para esta reação: ∆Hr°298
= – 163 kJ e ∆Sr°298
= 148 J. K-1
Qual o valor de KP para
esta reação a 80 ºC?
Resolução
T = 80 ºC = 353 K
∆G°353 = ∆Hrº298
– 353 K x ∆Srº298
∆G°353 = – 163 000 J
– 353 K x 148
J. K-1
∆G°353 = – 163 000 J
– 52 244 J
∆G°353 = – 215 244 J
KP = e –
(∆G° / RT)
KP = e –
(– 215 244 / (8,314x353)
KP = e 73,34
KP = 7,10 x 1031
|
Fonte: Instituto de Química da Universidade Federal do Rio Grande
do Sul |